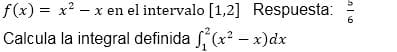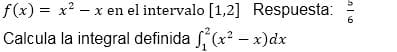$$\begin{align}&\int_{1}^2 (x^2-x) dx\\&a=1\\&b=2\\&\Delta x = \frac{b-a}{n}=\frac{1}{n}\\&x_i=a + i \Delta x = 1 + \frac{i}{n}\\&f(x_i) = x_i^2-x_i =(1+\frac{i}{n})^2-(1+\frac{i}{n})=1+\frac{2i}{n}+\frac{i^2}{n^2}-1-\frac{i}{n}=\\&=\frac{i}{n}+\frac{i^2}{n^2}=\frac{i^2+i n}{n^2}\\&Retomando...\\&\int_{1}^2 (x^2-x) dx = \lim_{n \to \infty} \sum_{i=1}^nf(x_i)\Delta x=\\&\lim_{n \to \infty} \sum_{i=1}^n \frac{i^2+i n}{n^2} \frac{1}{n}=\lim_{n \to \infty} \frac{1}{n^3} (\sum_{i=1}^n i^2+i n)=\\&\lim_{n \to \infty} \frac{1}{n^3} (\sum_{i=1}^n i^2+ \sum_{i=1}^n i n)=\lim_{n \to \infty} \frac{1}{n^3} (\sum_{i=1}^n i^2+ n\sum_{i=1}^n i )=\\&\lim_{n \to \infty} \frac{1}{n^3} (\frac{n(n+1)(2n+1)}{6}+ n \frac{n(n+1)}{2} )\\&\text{Cuando n} \to \infty\\&\to (\frac{2}{6} + \frac{1}{2}) = \frac{5}{6}\end{align}$$Vamos con Riemann entonces...
Salu2...