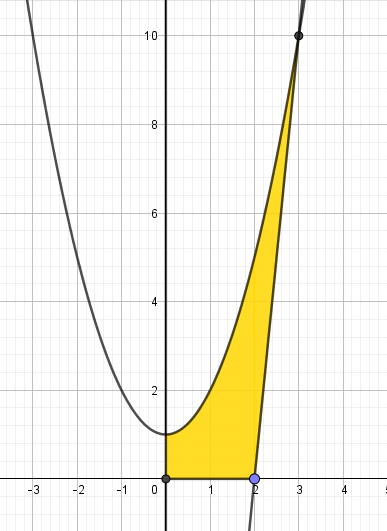
Apoyo para resolver este problema por el método de arandelas (sólidos de revolución)
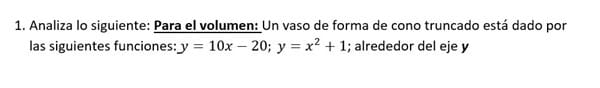
a)- Analiza con respecto a qué se integra, considerando que es alrededor del eje y; y encuentra los puntos de intersección o el par ordenado (x, y).
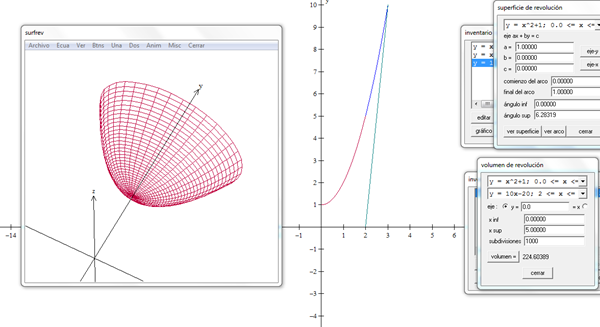
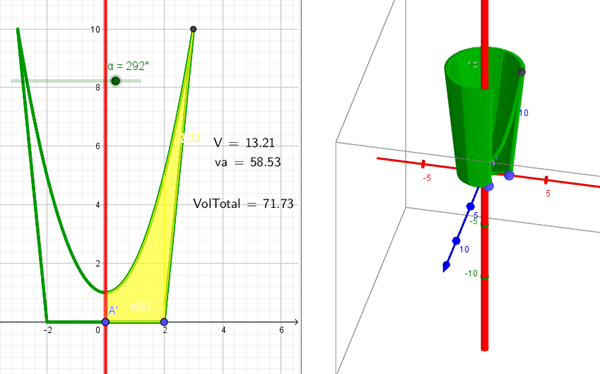
b)- Gráfica en 3D las funciones (puede ser en Excel o Geogebra):
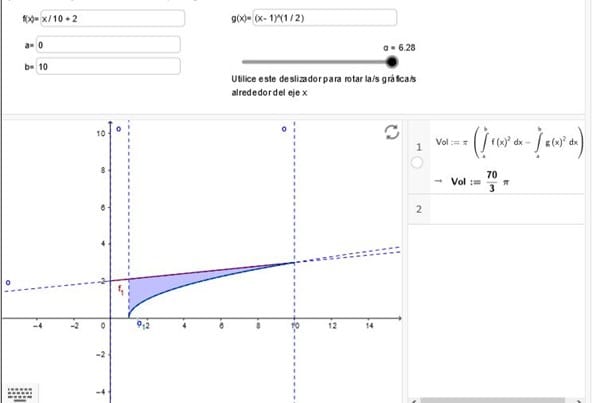
c)- Resuelve por el método de las arandelas (sólido de revolución) y encuentra el radio exterior y el radio interior.
d)- Encuentra el volumen necesario para construir el vaso.
1 respuesta
Respuesta de Lucas m
1