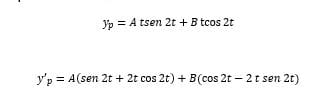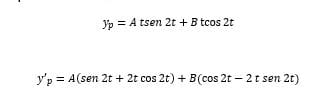Resolver ecuación diferencial no homogénea de orden superior
En la siguiente imagen se describe un problema de ecuaciones diferenciales de orden superior para su solución paso a paso.
La respuesta es la A
Como la pregunta se centra en la solución particular, no hará falta realizar la solución asociada
Entonces para hallar la solución particular nos fijamos en el tipo de función que esta al lado derecho, en este caso y proponenos una solución en la que pondremos una constante por el seno t y otra constante por el cos t (siempre se debe colocar seno y coseno cuando tenemos una función trigonométrica de la forma seno o coseno según el caso) y luego derivamos dos veces ya que es una ecuación de segundo orden
Proponemos pues
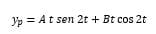
Ya que es una función del tipo seno, (usamos coeficientes indeterminados)
Ahora lo que hacemos es sustituir esta solución particular en nuestra ecuación y para esto necesitamos saber la segunda y primera derivada
Calculamos la primera derivada
