Utilizando derivadas cómo calcular si se inscribe un cilindro circular recto en una esfera de radio 𝑅 = 6 pulgadas

El área lateral del cilindro es igual al perímetro (p) de la base * h, es decir que depende de dos cosas: p y h.  Además, p=2π*r;  siendo r el radio del cilindro. Para optimizarla tenemos que hacerlo depender de una sola: es decir, hacer que "una dependa de la otra".

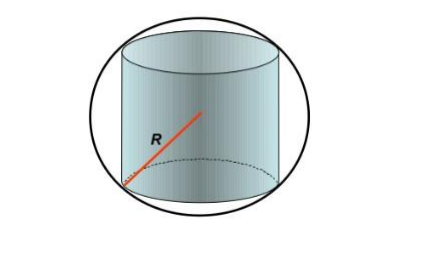
Si hacemos un corte que pase por el centro de la esfera y por el eje del cilindro, podemos generar un triángulo rectángulo cuyos lados sean "r" (radio del cilindro) y h/2 (mitad de la altura del cilindro). El radio de la esfera (R=6) es la hipotenusa. Por Pitágoras:

6^2 = (h/2)^2 + r^2;  con lo que podemos "hacer depender h de r".

(h/2)^2 = 36 -r^2;  

h = 2*√ (36-r^2).   Reemplazo en el área lateral:  A=2π*r * h, quedando:

A=2π*r* 2*√ (36-r^2);  o:

A=4π * [r*√ (36-r^2)];  derivo (como producto) para optimizar el área:

dA/dr =4π * { √ (36-r^2) -    [r^2 /√ (36-r^2)] }; 

dA/dr =4π * { (36-r^2) -    r^2 } /√ (36-r^2);

dA/dr =4π * { (36-2r^2)} /√ (36-r^2);  igualo a 0:

0 = 36 - 2r^2;    o:  0 = 18-r^2;  

r^2=18;  

r= 3√2;  que es tu radio del cilindro optimizado.

De  h = 2*√ (36-r^2),  reemplazo:

h = 2√2