Área de un triangulo a partir de estos datos

La verdad que no encuentro las fórmulas que hay detrás de esto, pero está claro que la respuesta es 24

Ahora te voy a ampliar la respuesta con la teoría.

Lo primero que voy a hacer es definir el punto D, que sea el punto donde se cortan las 2 secantes y luego defino las áreas x, y como muestra el gráfico (x+y es justamente lo que queremos averiguar para sumarlo al resto del triángulo para hallar el área total).

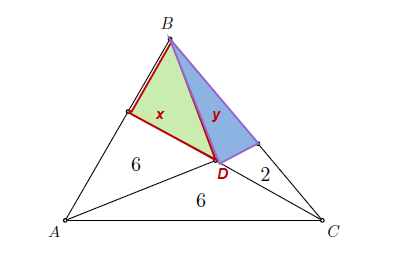
Si miramos al triángulo como si tuviese base AB, entonces 

$$\begin{align}&\frac{y+2}6=\frac{x}{6} \to x = y+2\\&\frac{x+6}6=\frac{y}{2} \to x+6=3y\\&Resolviendo\ el \ sistema\\&y=4, x=6\\&Area\ total = 4+6+6+6+2=24\end{align}$$

Que efectivamente coincide con lo que te había pasado, pero ahora demostrado.

Te dejo un video con un ejercicio similar, solo que cambiando los valores AQUI

Ahora sí va la teoría para demostrar que el área es 24

Lo primero que quiero que veas es la figura donde incluí un punto donde se cruzan los segmentos interiores y separé el área incógnita en dos áreas más pequeñas.

$$\begin{align}&\frac{y+2}6=\frac{x}6 \to x=y+2\\&\frac{x+6}6=\frac{y}2 \to x+6=3y\\&Resolviendo\ el \ sistema\\&y=4, x=6\\&Area\ total = 4+6+6+6+2=24\end{align}$$

Te dejo un link a un video con un problema similar, solo que con otros valores, AQUI