Encontrar el rango de las siguientes funciones

Te hago solo uno. Recuerda evaluar todas las preguntas que tienes pendiente (de todos los expertos).

$$\begin{align}&a) f:[-1,5[ \to R / f(x)=x^2-4x+3\\&\text{busco el foco (para eso busco primero las raíces)}\\&Raíces:\text{ A simple vista se ve que son: }r_1=1 \land r_2=3\\&\text{Como sabemos que la coordenada x del foco, está entre las raíces}\\&x_f=2 \to y_f=f(2)=-1 \to Foco:(2,-1)\\&\text{El foco será el menor valor que tenga la función, a partir de allí crecerá tanto para valores menores como }\\&\text{mayores de x}\\&\text{Como el foco está ligeramente hacia la izquierda del rango que nos dieron, el mayor valor estará }\\&\text{a la derecha (en x=5)}\\&f(5)=8\\&\text{Pero el 5 no forma parte del dominio, por lo tanto el rango será}\\&Rango: [-1, 8[\end{align}$$

1) Son muchos ejercicios para una sola pregunta, la idea es que te ayudemos con alguno como para que veas como se hace y luego intentes resolverlos vos (y pregunta dudas, no esperes todo el desarrollo)

2) Como ya dije, califica todas las preguntas pendientes.

Disculpe en el literal c) como hago. Para encontrar el rango

$$\begin{align}&.\end{align}$$

Te lo planteo de una forma, aunque no sé cual es tu nivel. Para esto voy a suponer que sabes derivar y lo que representa la derivada (si no es así, avisa y buscamos otra manera).

$$\begin{align}&f:[-1,2[ \to R/f(x)= 1 + \sqrt{3+2x-x^2}\\&f'(x)=\frac{1}{2 \sqrt{3+2x-x^2}}\cdot(2-2x)\\&f'(x)=0 \to x=1 (\in Dominio)\\&x \in [-1,0[ \to f'(x)>0 \to f(x) crece\\&x \in ]0,2[ \to f'(x)<0 \to f(x) decrece\\&\text{Por lo tanto para ver el rango vamos a ver cuanto vale la función}\\&\text{En el máximo y cuanto en los extremos del intervalo del dominio}\\&f(-1)=1 + \sqrt{3+2 \cdot (-1)-(-1)^2}=1\\&f(1) =1 + \sqrt{3+2 \cdot 1-1^2}=3\\&f(2)=1 + \sqrt{3+2 \cdot 2-2^2}=1+\sqrt{3}\\&\text{Conclusión: }Rango:[1, 3]\end{align}$$

Te dejo la imagen para que veas como quedaría donde se ve claramente el rango

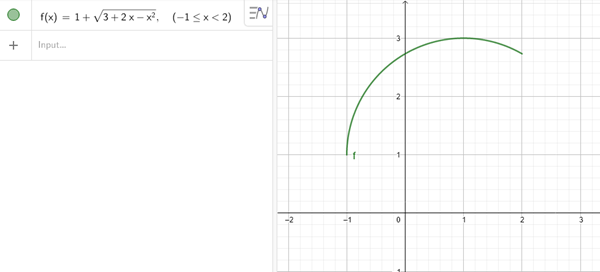
entonces el en literal f) igual me toca sacar la derivada para encontrar el rango sisque no me equivoco.

Correcto, aunque tiene dos diferencias con el que te pasé recién y es que:

1) La raíz está restando en lugar de sumar (lo que hará que la gráfica te quede 'al revés')

2) Ahora se trata de todos los reales, por lo que vas a encontrar un punto que sea mínimo (ya que al estar la gráfica al revés que la anterior, en lugar de un máximo hallarás un mínimo) y a partir de ahí como el dominio son todos los reales, la función crecerá indefinidamente hacia los infinitos

Y tal vez hay otra forma de sacar el rango sin hacer una derivada

Pues analíticamente no se me ocurre, si hacés la gráfica por supuesto que la podés deducir de ahí, pero eso en cierto modo es 'hacer trampa' ya que para hacer la gráfica más o menos bien, en realidad también deberías hallar máximos, mínimos, etc por lo que también deberías calcular la derivada

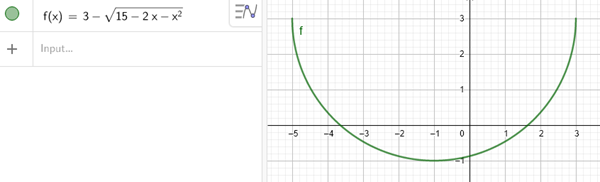
$$\begin{align}&f´\left(x\right)=\frac{1+x}{\sqrt{-x^2-2x+15}}\end{align}$$

disculpe esta bien sacada la derivada de el ejercicio f.

Me podría ayudar con el f) no me sale

La derivada está bien calculada, verás que se hace 0 en x=-1, por otro lado también son puntos de interés los valores x=3, x=-5, ya que es donde la derivada se anula y aprovecho para decirte que si bien la función viene definida para todos los reales, en realidad hay que restringirla a los valores 'válidos' y esto es donde está definida la raíz cuadrada (para valores mayores o iguales que 0), si haces el análisis verás que el dominio de la función (la original) es [-5, 3]

Intenta avanzar con esto más lo que ya desarrollaste.

me salió que el rango es y pertenece a [-1;3] estoy bien ?