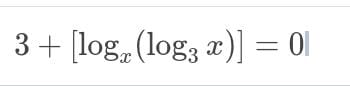Como resuelvo el siguiente ejercicio
Como resolver la siguiente ecuación logarítmica, por favor me pueden ayudar
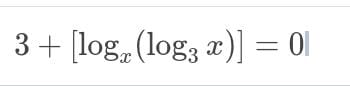
1 respuesta
Respuesta
1
Veamos si llegamos a algo...
$$\begin{align}&\text{Debes saber que } a^{log_a(b)}=b\\&3+log_x(log_3(x))=0\\&log_x(log_3(x))=-3\\&log_3(x)=x^{-3}\\&x = 3^{x^{-3}}\\&x = 3^{-3^x}\\&x = \bigg(\frac{1}{3}\bigg)^{3^x}\\&x = \bigg(\frac{1}{27}\bigg)^{x}\end{align}$$A partir de ahí, se me ocurren resolverlos por métodos analíticos (recursivos, del estilo del algoritmo de Newton-Raphson)
Más allá de los métodos iterativos que podrían ser usados en casos generales. En este caso se ve que x = 1/3 cumple la condición
Perdón, cometí un error en uno de los pasos del despeje...
$$\begin{align}&x = 3^{x^{-3}}\\&\text{Hasta acá estaba bien, el siguiente paso era el que estaba mal...}\\&x = 3^{\frac{1}{x^3}}\end{align}$$y acá sí que no veo como resolverlo algebraicamente sino que solo veo la opción de resolverlo analíticamente (por ejemplo con Newton-Raphson).
Si lo graficás ves que el resultado es aproximadamente 1.4422, pero no veo forma de llegar algebraicamente a ese valor...