En una viga en ménsula de una marquesina de hormigón. ¿Dónde se aplica el punto de aplicación?

Con las debidas reservas, y simplificando mucho.

Caso 1.- Si la estructura tiene sólo un pilar con una viga que nace de él en ménsula, y sobre la que actúan algún tipo de cargas, el momento es el resultado de multiplicar la carga por la distancia desde su punto de aplicación hasta el eje del pilar.

Caso 2.- Si la ménsula forma parte de una viga, apoyada en el pilar que comenta y en otro, entonces el valor del momento es el mismo, pero se reparte entre el pilar y el resto de la viga. Dicho de otro modo, el esfuerzo de flexión a que está sometido el pilar es mucho menor puesto que le "ayuda" la viga que no está en ménsula.

Si tiene alguna duda me vuelve a preguntar.

Puntualizo, lo explico como yo lo veo y espero no decir nada erróneo: me remito al caso 1.

La viga ménsula no vuelca porque "tira" de ella la armadura del pilar más alejada, con un brazo de palanca aplicado en el eje de la zona comprimida del pilar, y que yo sepa, EN ESTE CASO, dicho eje no está en el centro del pilar. Si se considera en el eje del pilar, creo que va del lado de la seguridad, pero mi duda es si es correcto hacerlo como yo digo. Por favor, y para no liarme más de la cuenta, contésteme SÍ o NO, y después de ello, si lo considera oportuno se extiende lo que considere necesario.

Tenga en cuenta que no soy titulado, y quizá las respuestas demasiado técnicas me cueste entenderlas. De todas las maneras, la suya la he entendido perfectamente, porque así estaba explicada.

Si.

Pero debe tener en cuenta que las armaduras no trabajan como si se tratase de cuerdas embutidas en el hormigón. Como todo en las estructuras, se ayudan unas a otras.

La ménsula no vuelca por la acción conjunta de la armadura que usted dice, que "tira" y la de la cara opuesta del pilar que se "comprime"

La primera armadura tiende a estirarse bajo la carga de la ménsula y la otra tiende a encogerse bajo esa misma carga.

La armadura que se "estira" tiene impedido ese "estiramiento" por la acción del hormigón que la rodea. De igual forma, la armadura que se comprime no puede hacerlo porque el hormigón que la rodea lo imposibilita.

No olvide que la mayor parte de la carga la absorbe la sección sin armaduras del hormigón y el acero es un mero refuerzo para cuando el hormigón está sometido a "estiramientos" que no podría soportar.

Como sabe, el hormigón en masa ( sin armar ) resiste muy bien esfuerzos de compresión como los de los pilares, pero no resiste casi nada los esfuerzos de tracción ( vigas ) por eso es preciso disponer una armadura que le "ayude" a resistir.

Espero haberme explicado. Si lo desea me vuelve a preguntar.

Gracias por la contestación. Creo que le he entendido. Para comprobarlo, me permito la siguiente exposición:

Supongamos que me dan un plano con los detalles de secciones, luz, armaduras, características de los materiales y cargas de la viga ménsula y pilar donde se empotra. Supongamos que el pilar no recibe otra carga que la que le transmite la viga. No hay empujes de tierras, no hay acciones de viento, no hay nada de nada más que lo expuesto. En una palabra, esto sería como una Linvertida (prescindo del cimiento, porque para lo que quiero saber, creo que no me hace falta). Supongamos que me piden comprobar que la viga (solo la viga) no vuelca. Lo haría de la siguiente manera:

1 Calculo el momento de la viga (Md).

2 Calculo la profundidad del hormigón comprimido (a).

3 Calculo el brazo de palanca (z).

4 Calculo el momento último resistente del pilar (tensión de las barras, minoradas x brazo de palanca) (Mu)

Conclusión: Si Mu > Md la viga no vuelca. ¿Está bien como lo he hecho?

Le respondo.

1.- Calcula el momento flector a que somete la ménsula al pilar.

2.- Calcula el momento resistente de la sección bruta del hormigón, sometida a flexión pura.

3.- Calcula el refuerzo necesario de armadura a colocar en la sección para que resista el esfuerzo.

4.- Si con la armadura resiste en flexión, sin plastificar, le vale. En caso contrario, modifica la sección de hormigón y vuelve a hacer los cálculos.

Lo mejor es apoyarse en un programa de cálculo que le haga los números. Pues en caso contrario, debería hacerlo por un método iterativo como el método de Cross.

De nuevo por aquí. Debo disculparme por mi "desaparición". Ha sido debida a problemas con el ordenador (¡lo he bloqueado!), y a que mi salud no ha sido del todo buena. Solventadas ambas cuestiones, continuo con mis dudas.

En mis últimas preguntas faltaban palabras que las completaran, ejemplo: 2.- Calculo la profundidad del hormigón comprimido (a) DEL PILAR. 3.- Calculo el brazo de palanca (z) CORRESPONDIENTE, DEL PILAR.

A sus respuestas, me surgen las siguientes dudas: 1.- El momento flector a que somete la ménsula al pilar, ¿es el producto de multiplicar la carga que recibe la ménsula por la distancia desde su punto de aplicación al eje de la zona comprimida del hormigón del pilar?, ¿o la distancia es hasta la cara del pilar?, ¿o el momento flector del que estamos hablando es otra cosa? 2.- El momento resistente de la sección bruta del hormigón ¿cómo se calcula? ¿tiene algo que ver con la zona comprimida del hormigón? 3.- El refuerzo de armadura necesario ¿sería el resultado de dividir el momento a que somete la ménsula al pilar entre el brazo de palanca? 4.- Aquí me he perdido: ¿qué quiere decir "sin plastificar"?

Insisto en que no soy titulado y me cuesta en ocasiones comprender los términos con los que usted se expresa. Mi intención es simplemente comprender "algo" (de momento) el funcionamiento de lo que pregunto, limitarme a ello y no profundizar (también de momento)demasiado en el tema, para poder comprenderlo. Pongo por ejemplo, que si estoy aprendiendo a sumar, hago una pregunta relativa a eso, y se me contesta con un problema de multiplicación, dificilmente voy a comprender ni la una ni la otra. Por ello mi pregunta se quiere referir sólo a cómo se consigue que la MÉNSULA (y solamente ella) no "gire" (no vuelca, decía yo anteriormente) sobre el eje de aplicación de las fuerzas que componen la palanca, y sobre todo, el lugar en donde se encuentra dicho eje (el teórico, el estricto).

Programas de cálculo no sé manejar. Por otra parte, lo que me interesa es "hacer números" para así aprender.

Me fijo ahora en lo mal que está redactado parte del título de encabezamiento de estas preguntas, que dice ¿DONDE SE APLICA EL PUNTO DE APLICACIÓN?. (Si sustituyo "aplica" por "situa", queda mejor ¿no?)

Gracias por su atención, y espero no ser demasiado "pesado" con mis preguntas. Un saludo.

No soy un profesor de cálculo de estructuras. Tan sólo un arquitecto que calcula estructuras y que cree tener claros algunos conceptos sobre el tema. Quizá mi lenguaje no sea todo lo claro que debería. Le pido disculpas por ello.

El cálculo de una estructura requiere, aunque se trate de algo tan sencillo como lo que me propone, unos profundos conocimientos de estática y matemáticas, luego aplicados a la resistencia de materiales.

En la carrera de arquitectura, se dedican cuatro años con distintas asignaturas a saber los fundamentos de ello.

No es fácil para mí responderle sin entrar en profundidades. Le repito que no soy maestro y que estudié el tema hace ya muchos años.

Intento contestarle aunque si le interesa el tema, lo mejor es que preguntara cosas más fundamentales.

1.- El momento flector que produce la ménsula al pilar es el resultado de multiplicar el valor de la carga que actúa sobre ella, por la distancia desde el punto de aplicación hasta el centro de gravedad del pilar. Su fórmula es M = P X l, siendo M el momento flector, P la carga y L la distancia desde el punto de actuación de la carga al centro de gravedad del pilar. Esto para el supuesto de carga puntual.

2.- En función de la relación de rigideces del nudo formado por la ménsula y el pilar, el cual se calcula en tanto por ciento una vez hallados los momentos de inercia de las secciones, el momento se "reparte" entre la sección de la ménsula y la del pilar.

A su vez, el momento que recibe el pilar en la cabeza o punto cercano a la ménsula, se reparte entre él y el empotramiento de la zapata.

Para calcular estos valores a mano, se realiza un proceso iterativo de reparto, que se conoce como método de Cross. Hacerlo a mano lleva no menos de media hora mientras que un programa de cálculo emplearía dos segundos.( No lo hace por Cross sino por matrices)

3.- Una vez conocidos los esfuerzos, se calculan las secciones.

El módulo resistente de una sección rectangular, a flexión simple, viene determinado por una expresión bastante compleja.

4 Una vez determinado el módulo resistente, se divide entre el momento y se obtiene la profundidad de la fibra neutra y, con ello se sabe si la sección plastifica o no.

Para no seguir enrrollándome, si le parece oportuno, me plantea un problema y yo se lo calculo, o me plantea alguna cuestión más sencilla e intento explicársela, aunque como vé, será difícil.

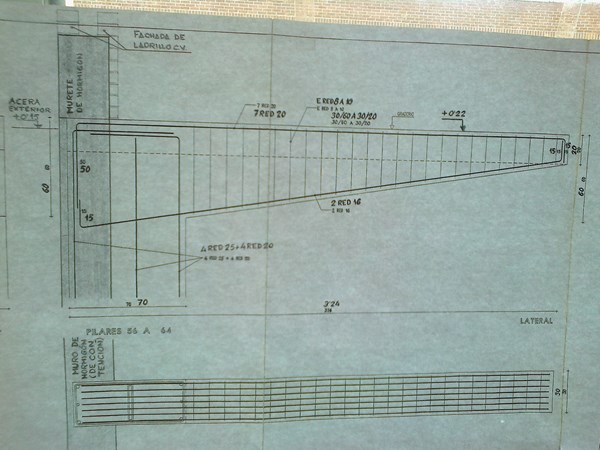
Gracias por su contestación. No es su culpa que no entienda algunos términos. Soy yo, por mi poca formación. Me parece una buena idea plantear un problema concreto, usted lo calcula, yo veo los números hechos, y así es posible que llegue a comprender mejor el tema. Dispongo de un plano, correspondiente a una obra en la que trabajé, en el que tengo la ménsula y pilar en cuestión ya calculados, por supuesto, pero en mi afán de aprender quiero saber cómo se ha llegado a ese resultado. Es un polideportivo, rectangular, con un muro de contención de hormigón en su perímetro, de 30 cm, desde la cota -2,73 hasta la + 0.22, con zapata corrida de 2,20, centrada; el canto lo desconozco. En uno de los lados largos es donde están las ménsulas que soportan la losa. Los pilares de los cuales salen las ménsulas están embutidos en el muro, de tal manera que de los 70 cm, 45 sobresalen hacia la cancha y 25 están dentro (el muro tiene 30, pero el pilar entra en él 25). Las zapatas de los pilares están embutidas en la del muro, son de 1,80x1,80, centradas con la del muro; el canto lo desconozco.

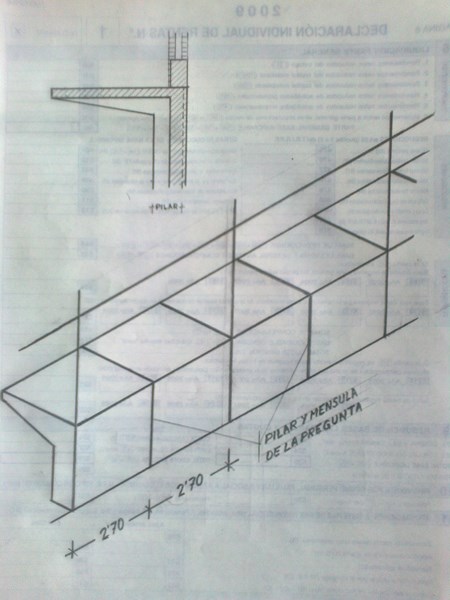
Se trata de varios pilares de 70x30 (70 en el sentido de la ménsula), separados 2,70 entre ejes, con 1 barra de 25 en cada esquina, más 1 barra de 20 en el centro de cada cara, de los cuales salen las ménsulas. Los pilares impares mueren a la cota +0,22 (son los que propongo como pregunta). Los pares llevan otro pilar rectangular de 60x25, con otra armadura diferente, este embutido totalmente en el muro, perpendicular a la ménsula y formando una T con el de 70x30 hasta la cota +0,22; a partir de ahí continúan hacia arriba solamente los de 60x25, para soportar las cerchas de la cubierta, que están a 5,40 entre ejes. Por encima de la cota +0,22, y con una altura de 50 o 60 cm y anchura de 31 cm, encima del muro de contención, hay un murete de hormigón armado, y encima de este la fachada de ladrillo. La sección de la ménsula es 60 de alto x 30, junto a la cara del pilar, y va reduciendo a 20 de alto x 30, en punta. Esta ménsula soporta una losa de 20 cm. La ménsula lleva 7 barras de 20 arriba y 2 de 16 abajo.

Datos: _Cota coronación de zapata de muro y de pilar - 2,73.

_Cota terminación muro de contención, pilar, ménsula y losa + 0,22.

_Cota pavimento cancha -2,48.

_Cota pavimento exterior +0,15.

_Luz ménsula (desde la punta hasta la cara interior del pilar) 2,54.

_Desde la punta de la ménsula hasta la cara exterior del pilar 3,24.

_Desde la punta de la ménsula hasta la cara exterior del muro 3,29.

_Separación, entre ejes, de las ménsulas 2,70.

_Pavimento de terrazo, 10 cm.

_Barandilla metálica en la punta.

_Sobrecarga de tabiquería, no hay.

_Sobrecarga de uso, la correspondiente a un polideportivo.¿Puede que sean 500 kg?

¿O es más?

_Hormigón H-200, coeficiente de seguridad 1,5.

_Armaduras AEH 500N, límite elástico (Fyk) 5100, coeficiente de seguridad 1,15.

_Acciones, coeficiente de seguridad 1,6.

_Recubrimientos, lo desconozco, pero supongo que serán 3 cm. ¿Quizá 4?

Bueno, queda demostrado que para enrollarse no hay otro como yo. Espero no haberme dejado ningún dato importante. Le ruego me disculpe. Saludos y gracias.

La he intentado seguir hasta que me he perdido, lo siento pero aunque usted lo hace muy bien, es muy difícil explicar una estructura sin planos.

Lo he ido dibujando en un croquis y no consigo entender la disposición de lo que me comenta.

Por otro lado, lo más importante para calcular una estructura, aparte de conocer su geometría, es conocer las cargas. No me dice las cargas de viento ni de sismo. No puedo deducir qué cargas gravitan sobre la ménsula y por lo tanto no puedo obtener los esfuerzos a los que está sometida la estructura.

Por otro lado, tampoco entiendo el proceso de montaje por si ello influyera en las cargas que van a soportar las ménsulas.

Como veo que tiene muchos conocimientos e interés, le propongo dos cosas; o me manda un correo con los planos, o lo que yo creo que es más fácil para los dos, me plantea una estructura sencilla, que pueda calcularle en media hora y se la explico con los resultados a la vista.

Piense que calcular lo que me ha pedido, cuando consiga entenderlo y estimar todas las cargas, es un proceso que lleva no menos de una semana de trabajo.

Para jojeanje:

Hace días le envié, siguiendo su sugerencia, a la dirección de correo [email protected] , haciendo notar en la casilla "Tema" que era un correo para jojeanje, y con título "Empotramiento de ménsula", unos dibujos del tema en cuestión. Al haber sido recientemente Semana Santa no me extrañó no recibir contestación. Pienso que no le ha llegado este correo. Espero sus noticias. Saludos.

No sé como recibirlo. Si lo consigo le contesto en cualquier caso.

jojeanje: le envío estos dos links como complemento a todo lo expuesto anteriormente.

Gracias por su atención. Un saludo.

Lo he visto y son planos muy antiguos. Hoy en día no se dibujan así las estructuras. De todas formas le repito que sin conocer las cargas no puedo hacer nada.

Le ruego me envíe algo más simple para que podamos hablar de ello si es su deseo. Lo que me ha mandado, encima sin cargas, puede llevanos un año de explicaciones que entiendo, superan con creces el objeto de una "pregunta por internet".

Buenas tardes jojeanje:

Le agradezco su interés. En el caso planteado lo que deseo conocer es cómo se calcula el pilar, y concretamente, haciéndolo poco a poco, de momento quiero limitarme a cómo se determina la excentricidad de la carga. Otro día preguntaré otra cosa. A ver si es como sigue:

Momento M = (3.200 x 2,90 x 2,90/2 + 540 x 2,90) x 1,6 = 24.035 kg (Mayorado por 1,6)

Cargas N = (3.200 x 2,90 + 540) x 1,6 = 15.712 kg (Mayoradas por 1,6)

Excentricidad = M/N = 1,53

¿Está bien?

De ser correcto lo que digo, creo estar, si no me equivoco, en un caso de flexión compuesta que, según Ehlers, "puede reducirse a un problema de flexión simple, sin más que tomar como momento el que produce el esfuerzo normal con respecto a la armadura de tracción". En este caso, ¿ el momento sería sustituyendo 2,90 por 2,90 + (0,65 - 0,70/2), o se incluyen también las cargas correspondientes a ese incremento de luz ?

Espero no estar molestando más de la cuenta. Muchas gracias. Saludos.

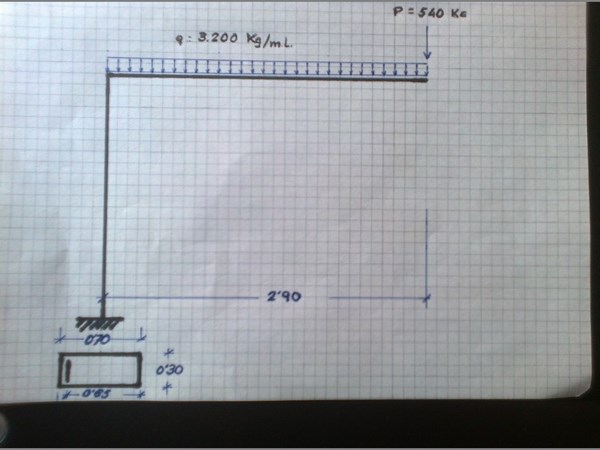
Haciendo unos números a mano, me sale que, debido a la carga puntual, en el encuentro entre la ménsula y el pilar hay unos esfuerzos como sigue:

momento = 1.566 mkg.

cortante = 540 kg.

En función de la carga distribuida, los esfuerzos son los siguientes:

momento = 13.456 mkg

cortante = 9.820 kg.

Los esfuerzos totales sobre el nudo son la suma de ambos

Ahora necesito saber las secciones y materiales de la ménsula y el pilar para redistribuirlos.

Hola, buenas tardes:

Le envío los datos solicitados.

Sección Materiales Coeficientes Armaduras Situación

Pilar 70*30 Acero AEH500N 1,15 4 barras de 25+ En las esquinas

4 barras de 20 En el centro de las

4 caras

Hormigón HA-200 1,5

Viga h*b=60*30 Acero AEH500N 1,15 7 barras de 20 Tracción

2 barras de 16 Compresión

Hormigón HA-200 1,5

Ejecución 1,6

Gracias por su atención.

Hola:

Se me olvidaba decir que en el dato dado de carga uniformemente repartida ya está incluido el peso propio de la ménsula, aunque quizá no se dibuje como lo he hecho.

Pronto le contesto. Ahora estamos un poco desbordados de trabajo. Siento hacerle esperar.

No se preocupe. Mientras tanto aprovecho para aumentar mis escasos conocimientos. Muchas gracias y ya contestará cuando pueda.

No he encontrado por ningún sitio la altura del pilar por lo que la he presupuesto de 3,00 m. Si es diferente me lo dice y rehago el cálculo.

Los resultados de un cálculo sencillo son los siguientes:

Pilar

70 x 30 cumple el hormigón

Armado con 4R16 en las esquinas. 4 R 12 en el centro de las caras y 2 R 12 como armadura de piel

Viga

60 x 30 cumple el hormigón

Armada con 4R16 + 2R10 arriba

2R12 abajo

2R10 de armadura de piel con estribos del 8 cada 30 cm.

Tenga en cuenta que no he calculado ni limitado flecha ni pandeo por lo que ya le digo que el cálculo es más un predimensionado.

Espero le valga. Ahora que ya lo tengo en el ordenador, me será más fácil hacer cambios si los requiere.

Muchas gracias por su contestación, pero cómo lo que pretendo es aprender, si no me dice cómo se llega al resultado que me da, no me va a valer de mucho. La altura del pilar es 2,95. Sigo entrando en Internet buscando información al respecto, y entre esto y sus respuestas por lo menos tengo bastante claro algunas cosas más, como por ejemplo la pregunta con la que inicié este tema. Estoy informándome sobre los "dominios de deformación", "cuantías balanceadas", "ductilidad de vigas", etc; poco a poco voy entendiendo el tema. Pero cuanto más me informo más dudas me surgen, por ejemplo: la sobrecarga variable a tener en cuenta en un local con aglomeración de público, como es un polideportivo, es 500 kg/m2. ¿Va incluido ahí la fuerza que genera el público al saltar al unísono en sus celebraciones? ¿Qué se hace para calcular una estructura a sismo?

Gracias por su atención.

Haber. Hasta aquí hemos llegado. Durante más de tres meses he contestado sus preguntas lo mejor que he podido.

No soy quien para enseñarle a usted estructuras, cálculo de estructuras o cosas semejantes. Tan solo soy un arquitecto especializado en la rama de edificación que calcula las estructuras de sus proyectos y que ha tenido que calcular en no pocas ocasiones estructuras difíciles o complejas.

No tengo los conocimientos suficientes como para darle una clase sobre estructuras con la responsabilidad que eso conlleva.

Por otro lado, no estaría de más que cerrase y puntuase mis respuestas pues al no hacerlo no contribuye para que aumente mi posicionamiento entre los expertos.

Por lo tanto le ruego, si es su parecer, que en lo sucesivo cierre esta pregunta, la puntúe y abra otras nuevas, tantas como desee, al objeto que mis respuestas obtengan la puntuación que usted desee ponerles.

En cuanto a la "sobrecarga variable" mejor dicho, la alternancia de sobrecargas, con ese valor se supone que están incluidos los saltos.

En cuanto a lo de calcular con sismo, es un tema muy complejo que en España apenas es preciso dado que la normativa al respecto excluye, para edificios normales, su aplicación en casi todo el territorio nacional.