Problema de física que incluye centro de masa
En un examen que tuve, incluyeron el siguiente problema:
Un bloque de masa m1=3.7 kg sore un plano inclinado sin fricción de 30° de angulo, esa conectado por un cordón sobre una polea sin masa y sin fricción a un segundo bloque de masa m2=2.3 kg que cuelga verticalmente. ¿Cuáles son la magnitud de la acelerecion de cada bloque, la dirección de la aceleración del bloque colgante y cual es la tensin de la cuerda?
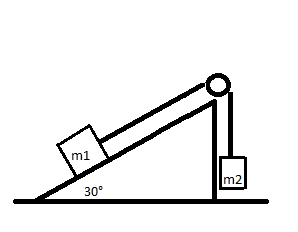
Lo primero que hice yo, fue suponer que la aceleración era la misma para ambos bloques y que a lo más, variaría en la dirección, no estoy segura si esto es correcto pues nunca pude confirmarlo, por otra parte, en la resolución del problema me dijeron que tenia que usar el centro de masa, aunque no entiendo de que...
Un bloque de masa m1=3.7 kg sore un plano inclinado sin fricción de 30° de angulo, esa conectado por un cordón sobre una polea sin masa y sin fricción a un segundo bloque de masa m2=2.3 kg que cuelga verticalmente. ¿Cuáles son la magnitud de la acelerecion de cada bloque, la dirección de la aceleración del bloque colgante y cual es la tensin de la cuerda?

Lo primero que hice yo, fue suponer que la aceleración era la misma para ambos bloques y que a lo más, variaría en la dirección, no estoy segura si esto es correcto pues nunca pude confirmarlo, por otra parte, en la resolución del problema me dijeron que tenia que usar el centro de masa, aunque no entiendo de que...
1 Respuesta
Respuesta de resnick
1


Por que la fuerza Normal no es tomada en cuenta para el objeto de masa 1???? - Anónimo