Ayuda con estática...
Espero mq puedas resolver estos ejercicios, tengo practica la otra semana y no salen, seria de gran ayuda que los puedas resolver..
Mi putnuacion sra excelente si puedes resolver estos ejercicio que no me salen, y tengo practica la semana que viene ... Ojala puedas
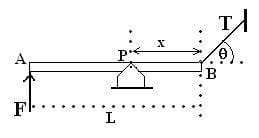
1.-1. La figura muestra una viga AB de peso despreciable y longitud L = 5m, en equilibrio. Si F = 500 N, T = 200 N y ? = 30°. Halle:
a) La reacción en el punto P
b) la distancia x
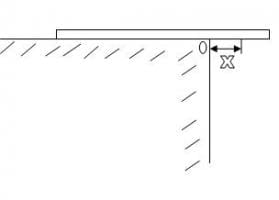
2.- Un tablón uniforme de 5m de longitud y 300N de peso descansa horizontalmente al borde de una azotea con 1.5m del tablón en el aire.
a) Dibuje el Diagrama de Cuerpo Libre del tablón.
b) Si después un pintor de 700N de peso, sube al tablón como indica la figura ¿Hasta qué distancia por puede avanzar éste justo antes de que se voltee el tablón?
c) Para la pregunta b) dibuje el diagrama de cuerpo libre del tablón.
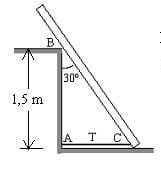
3.-1. Una barra homogénea de 1200 N de peso y de 2,0 m de longitud, descansa sobre un piso liso y sobre el borde liso B indicados en la figura. La barra esta atada a una cuerda AC que se encuentra cerca del piso. Determine:
a) DCL
b) La tensión T
c) Las fuerzas de reacción que ejercen el piso y el borde B sobre la
Barra.
Mi putnuacion sra excelente si puedes resolver estos ejercicio que no me salen, y tengo practica la semana que viene ... Ojala puedas
1.-1. La figura muestra una viga AB de peso despreciable y longitud L = 5m, en equilibrio. Si F = 500 N, T = 200 N y ? = 30°. Halle:
a) La reacción en el punto P
b) la distancia x

2.- Un tablón uniforme de 5m de longitud y 300N de peso descansa horizontalmente al borde de una azotea con 1.5m del tablón en el aire.
a) Dibuje el Diagrama de Cuerpo Libre del tablón.
b) Si después un pintor de 700N de peso, sube al tablón como indica la figura ¿Hasta qué distancia por puede avanzar éste justo antes de que se voltee el tablón?
c) Para la pregunta b) dibuje el diagrama de cuerpo libre del tablón.

3.-1. Una barra homogénea de 1200 N de peso y de 2,0 m de longitud, descansa sobre un piso liso y sobre el borde liso B indicados en la figura. La barra esta atada a una cuerda AC que se encuentra cerca del piso. Determine:
a) DCL
b) La tensión T
c) Las fuerzas de reacción que ejercen el piso y el borde B sobre la
Barra.

1 Respuesta
Respuesta de ricardonb
1
