Calcular extremos absolutos de una función

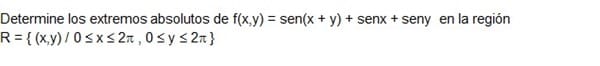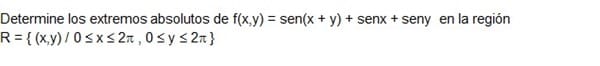
Este no es un problema de multiplicadores de Lagrange, es el típico problema de calcular máximos o mínimos de funciones de varias variables. Los multiplicadores de Lagrange son cuando hay una o varias ecuaciones que ligan el valor de las variables. Aquí lo que hay es una región cuadrada, lo mismo que en una variable sería un intervalo.

Si una función es diferenciable en un dominio, los máximos o mínimos absolutos están en los puntos críticos o en la frontera del dominio.

Primero veamos los puntos críticos derivando e igualando a 0

fx(x,y) = cos(x+y) + cosx = 0

fy(x,y) = cos(x+y) + cosy = 0

Se deduce cosx = cosy

Luego pueden ser dos casos

1) y=x

2) y=2pi-x

En el caso 1

cos(2x) + cosx = 0

cos^2(x) - sen^2(x) + cosx = 0

cos^2(x) - 1 + cos^2(x) + cosx = 0

2cos^2(x) + cosx -1 = 0

cosx = [-1 +- sqrt(1+8)]/4 = 1/2 y -1

x=pi/3, 5pi/3 y Pi

Los puntos críticos de este caso son

(pi/3, pi/3)

(5pi/3, 5pi/3)

(pi,pi)

En el caso 2

cos(x+2pi-x) + cosx = 0

cos(x+2pi-x) + cos(2pi-x) = 0

de la primera

1+cosx= 0 ==> x = pi

y x=pi cumple la segunda

Esto nos da el punto (pi,pi) que ya estaba antes

Luego los puntos críticos son

(pi/3, pi/3)
(5pi/3, 5pi/3)
(pi,pi)

Calculamos de valor de la función en ellos

f(pi/3,pi/3) = sen(2pi/3) + sen(pi/3)+sen(pi/3) = sqrt(3)/2+sqrt(3)/2+sqrt(3)/2= 3sqrt(3)/2

f(5pi/3,5pi/3) = sen(10pi/3) + 2sen(5pi/3) = -sqrt(3)/2 - sqrt(3) = -3sqrt(3)/2

f(pi,pi)= sen(2pi)+2sen(pi) = 0

Y ahora veamos que sucede en la frontera

En la frontera una variable vale 0 o 2Pi y la otra toma todos los valores, sin perder generalidad sea y la que vale 0 o 2pi

f(x,y) = senx + senx = 2 sen x

Esto puede tomar valores entre -2 y 2

Pero si hallamos los valores decimales de los puntos anteriores son 2,598076 y -2.598076 luego

El maximo absoluto es 3sqrt(3)/2 en el punto (pi/3, pi/3)

El mínimo absoluto es -3sqrt(3)/2 en el punto (5pi/3,5pi/3)

Y eso es todo.