Ejercicio sobre funciones! Matemática a!

a) La composición (fog)(x) se calcula sustituyendo en f(x) la x por g(x)

$$(fog)(x)=f(g(x))=\left(\frac 1x\right)^2+3\left(\frac 1x \right)=\frac{1}{x^2}+\frac 3x$$

b) La inversa de f se calcula despejando la por en la expresión y = f(x)
y = x^2+3x
x^2 + 3x - y = 0
Es una ecuación de segundo grado

$$x=\frac{-3\pm \sqrt{9+y}}{2}\\ \\ \text{Y ahora se vuelve a poner x donde y}\\ \\ f^{-1}(x) =\frac{-3\pm \sqrt{9+x}}{2}\\$$

Hay dos funciones inversas una para cada rama de la parábola que es f(x)
En concreto. El vértice está en por=-3/2
Para f(por) de (-oo, -3/2] ----> R la función inversa es la que tiene el signo - delante de la raíz
para f(por) de [-3/2, +oo) ---> R la función inversa es la que tiene el signo + delante de la raíz

c) Una función es par si f(x)=f(-x) y es impar si f(x) = -f(-x)
Dada f(x) = x^2+3x tenemos
f(-x) = (-x)^2 + 3(-x) = x^2-3x
no se cumple ninguna de las dos, luego f ni es par bi es impar
Dada g(x) = 1/x
g(-x) = 1/(-x) = - 1/x
Aquí se cumple g(x) = -g(-x) luego es impar.
d) La función h(x) supongo que has querido poner xe^x. Es muy importante usar el símbolo ^ antes de los exponentes, si no son factores por la derecha

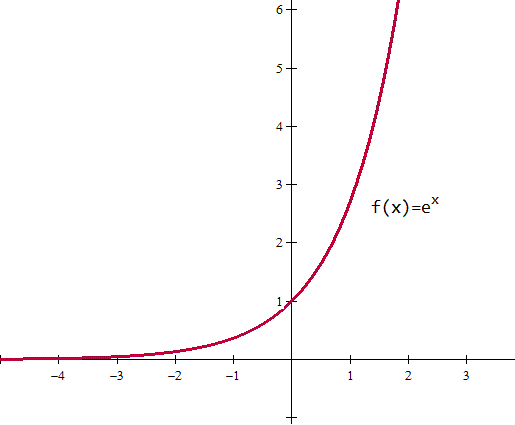
$$r(x)=g(x)h(x)=\frac 1xxe^x=e^x$$

Y ahora habría que hacer la gráfica de esa función archifamosa. No sé que te piden que calcules para hacer la gráfica pero:
Es una función continua definida en todo R, siempre positiva y creciente, cóncava hacia arriba, con asíntota horizontal y=0 en menos infinito y corta al eje Y en y=1

Y eso es todo.