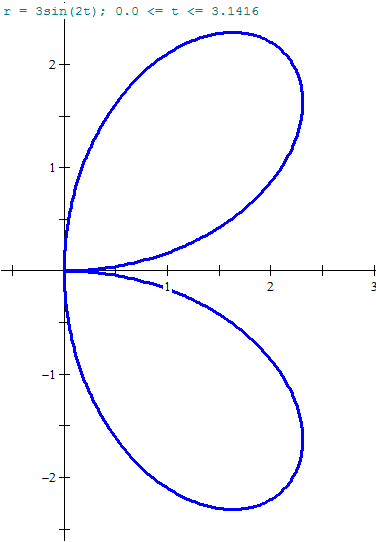Graficar la ecuación coordenadas polares

Antes se mando ella sola una pregunta de una curva que se parecía a un corazón. Mándala de nuevo para que la conteste

La curva es

r=3sen(2t)

Aquí no podemos escribír la letra griega theta esa y la sustituimos por la letra t.

Se hace la tabla para ciertos valores. Habría que usar el ángulo en radianes, pero como no nos vamos a enterar de nada lo usaré en grados mucho más fácil

T r
0 0
15º    3·sen(30º) = 3/2 = 1.5
22.5º  3·sen(45º) = 3sqrt(2)/2 = 2.1213
30º    3·sen(60º) = 3sqrt(3)/2 = 2.5981
45º    3·sen(90) = 3
60º    3·sen(120º) = 3sqrt(3)/2 = 2.5981 
67.5º  3·sen(135º) = 3sqrt(2)/2 = 2.1213
75º    3·sen(150ª  = 3/2 = 1.5
90º    3·sen(180º) = 0
105º   3·sen(210º) = -3/2 = -1.5
112.5º 3·sen(225º) = 3sqrt(2)/2 = 2.1213
120º   3·sen(240º) = -3sqrt(3)/2 = -2.5981
135º   3·den(270º) = -3
150º   3·sen(300º) = -3sqrt(3)/2 = -2.5981
157.5º 3·sen(315º) = -3sqrt(2)/2 = -2.1213
165º   3·sen(330º) = -3/2 = -1.5
180º 3·sen(360º) = 0

Luego esa serán las longitudes del radio vector para cada ángulo. Para ángulos mayores se vuelve a repetir la figura.

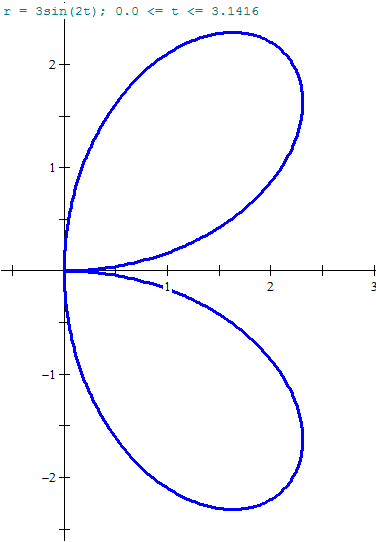
Y eso es todo.