Demostrar que la recta tangente que pasa por el punto de intersección que pasa por
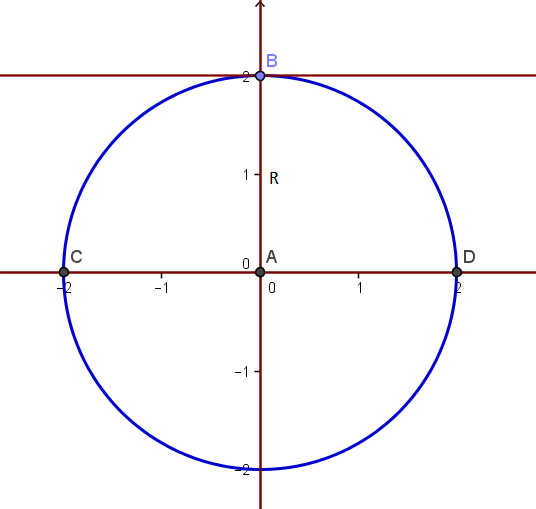
Sea C una circunferencia. El diámetro D de C tiene una mediatriz. Demostrar que
la recta tangente que pasa por el punto de intersección de la mediatriz y la
circunferencia C es paralela a la recta que contiene al diámetro D.
1 respuesta
L mediatriz del diámetro es una recta perpendicular al diámetro pasando por el centro del diámetro que es el centro de la circunferencia, luego la mediatriz contiene otro diámetro perpendicuolar al primero. Y como diámetro contiene dos radios. Ya hicimos un ejercicio donde demostramos que la tangente en el extremo del radio es penpendicular a este.
Todo ello podemos verlo en este gráfico. CD es el diámetro, la recta AB es la mediatriz, AB es un radio, luego la tangente en B es perpendicular a la recta AB
Luego tenemos que la tangente por B y la recta CD son ambas perpendiculares a la recta AB, y por lo tanto son paralelas entre sí.
Y eso es todo.
