Resuelve el problema dado, usando derivadas o integrales.
Sea p = (10-3x)^2
para x menor o igual entre 0 y 3
el precio el cual se venderán x
cientos de unidades
de cierto artículo, y sea R(x)=xp(x) el ingreso
obtenido de la venta
de las x unidades.
a) Encuentre el
ingreso marginal R´(x),
b) Dibuje las curvas
de ingreso y de ingreso marginal en la misma
gráfica.
c) ¿Para qué nivel de producción
se maximiza el ingreso?
1 respuesta
a) El ingreso marginal es la derivada del ingreso respecto de las unidades vendidas, x en este caso
R(x) = x·p(x) = x(10-3x)^2
Img(x) = R'(x) = (10-3x)^2 + x·2(10-3x)(-3) = (10-3x)(10-3x-6x) = (10-3x)(10-9x)
Img(x) = (10-3x)(10-9x)
¿Qué pasa con los profesores?
Que cuando la tenemos como factores la quieren ver como polinomio y cuando tenemos un polinomio quieren verla factorizada, el caso es trabajar. Vamos a ponerla como polinomio también
Img(x) = 100 -90x - 30x +27x^2
Img(x) = 27x^2 - 120x + 100
b) En rojo la función de ingreso R(x) y en azul el ingreso marginal Img(x)
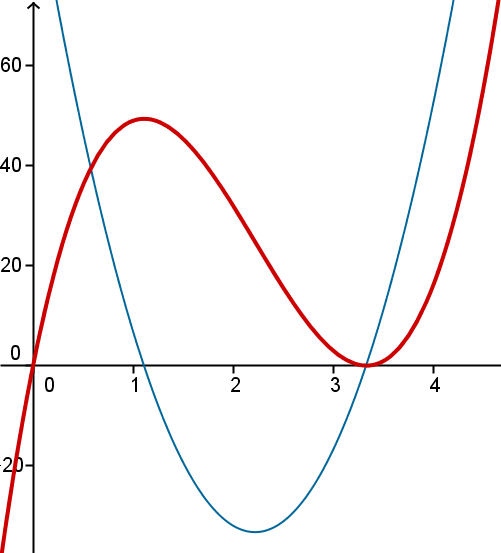
c) Se maximiza (o minimiza, que hay que comprobarlo) cuando la derivada de la función ingreso es nula, es decir, cuando el ingreso marginal es nulo.
Teniamos el ingreso márginal en forma factorizada que es ideal para calcular las raíces.
Img(x) = (10-3x)(10-9x)
Las raices son
10 - 3x = 0 ==> x = 10/3
10 - 9x = 0 ==> x = 10/9
Ahora habría que comprobar cuál es máximo o minimo. Con la gráfica ya vemos que el máximo está en 10/9. Pero si no hubiera gráfica calcularíamos la derivada segunda de R(x). Ahora me conviene más la forma polinómica de Img
R''(x) =Img'(x) = 54x - 120
Y vemos el signo que toma para los puntos críticos
R''(10/3) = 540/3 - 120 = 180-120= 60 es positiva y por tanto es un mínimo
R''(10/9) = 540/9 - 120 = 60-120 = -60 es negativa y por lo tanto es el máximo
Luego el nivel de producción que maximiza el ingreso es 10/9 = 1.1111111...
Hola! Antes que nada darte las gracias por el apoyo que brindas, en verdad se agradece!
Solo una duda, la CONDICIÓN al inicio del problema dice: que x es menor o igual entre 0 y 3, donde lo utilizas esto, en la gráfica? o en alguna parte del desarrollo del problema?
Gracias!
No, no le he empleado, se me olvidó.
Es la primera vez que me ponen un problema de estos con esa condición, no me di cuenta y lo hice como he hecho todos. Entonces lo que tienes que hacer es cortar la gráfica y solo tendría lo comprendido entre x=0 y x=3.
Ya antes tendría que haber quitado la parte de antes del 0 porque esa no vale nunca pero no lo hice porque el programa de gráficas que usé no permite establecer el dominio de la gráfica.
Y luego solo habría un punto crítico que sería 10/9 ya que 10/3=3.33333 se sale del intervalo.
De todas formas nunca está de sobra comprobar que la derivada segunda es negativa para confirmar que es un máximo. He visto muchos ejercicios que me mandan que fallan en cosas tan simples como que la función ingreso es negativo.
Y eso es todo.
