Calcular integral siguiente...
$$I=\iint_C{\left(\frac{x-1}{x(3-y)^2}\right)}dxdy$$donde
$$C\in: x+y\leq4,xy\geq3$$
A)
$$\begin{align}&ln2-\frac{3}{4}\\ &\end{align}$$B)
$$ln3-\frac{2}{3}$$C)
$$\frac{4}{3}-ln3$$D)
$$\frac{3}{2}+ln2$$Como te echaba de menos!!!! Muchas Gracias!!
1 Respuesta
Nada como una gráfica para entender el intervalo de integración
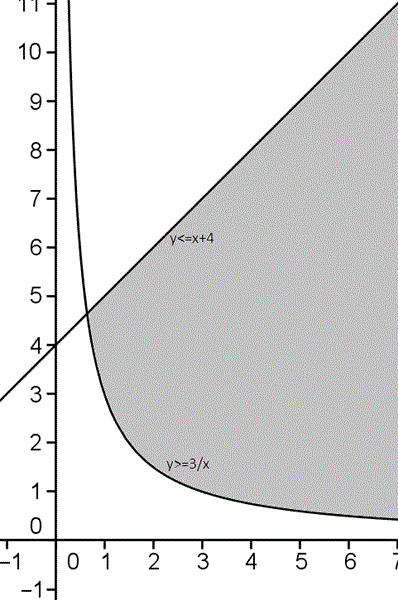
Algún día aprenderé a hacerlos más pequeños. Bueno no se ve, pero el intervalo es infinito, luego tendremos una integral impropia. En Y esta limitador por las funciones y=3/x, y=x+4. En x tendremos que hallar el punto donde se cortan
3/x = x+4
3 = x^2+4x
x^2+4x-3=0
x = [-4+-sqrt(16+12)]/2= [-4+sqrt(28)]/2 = -2+sqrt(7)
$$\begin{align}&I=\iint_C{\left(\frac{x-1}{x(3-y)^2}\right)}dxdy=\\ &\\ &\\ &\int_{3/x}^{x+4} \int_{-2+\sqrt 7}^{+\infty}\left(\frac{x-1}{x(3-y)^2}\right)dxdy =\\ &\\ &\\ &\int_{3/x}^{x+4} \left( \lim_{k \to +\infty} \frac{1}{(3-y)^2}\left [x-ln \;x \right ]_{-2+\sqrt 7}^k \right )dy=\\ &\\ &\\ &\\ &\int_{3/x}^{x+4} \left( \lim_{k \to +\infty} \frac{1}{(3-y)^2}\left [k-ln\;k+2-\sqrt 7+ln(-2+\sqrt 7) \right ]_{-2+\sqrt 7}^k \right )dy=\end{align}$$Y ese límite es infinito, luego la integral es divergente. Ya no podemos continuar.
Si el enunciado era ese, la integral es divergente.
Y eso es todo.
Lo de la gráfica, una pasada!
Ha sido super fácil ver todo, pero al no darte ninguna solución, he indagado un poco y creo que una de las funciones por las que está limitado no es y=x+4, si no por y=4-x.
Así el intervalo de integración es finito, desaparece la integral impropia y es mucho más simple de calcular. También obtengo una solución, la B.
Muchísimas gracias y como siempre, Excelente!
