Factorizar una ecuación de orden 5to

Si has estudiado algo de matemática superior sabrás que no hay método general para solucionar las ecuaciones de grado 5 o superior. Aparte que las de grado 3 son muy difíciles y las de grado 4 prácticamente imposibles en la práctica.

Si los problemas están preparados con raíces enteras e incluso racionales existen algunos métodos para hallar la respuesta exacta o base de probar y probar.

Se sabe que el producto de las cinco raíces es el término libre del polinomio, luego es 8.

Si hubiera una raíz entera sería un divisor de 8, eso limita las posibilidades a

{1, -1, 2, -2, 4, -4, 8, -8}

p(x) = x^5 - 4 x^3 - 4 x^2 - 4 x + 8

p(1) = -3

p(-1) = 11

es una tarea pesada a partir de aquí, la haré con calculadora

p(2) = -16

p(-2) =0

luego -2 es una raíz, ahora usamos Ruffini para hacer la factorización

     1   0  -4  -4  -4  8
-2      -2   4   0   8 -8
     --------------------
     1  -2   0  -4   4 |0

Luego la factorización es

(x+2) (x^4 - 2x^3 - 4x + 4)

Y aquí se acabo lo bonito ya no hay más respuestas enteras

Si el problema fuera de teoría veríamos que el polinomio de grado cuatro que queda es positivo en 0 y en 1 es negativo

p(0) = 4

p(1) = -1

Luego entre 0 y 1 hay una solución real

Usaríamos el método de Newton por ejemplo para aproximar la respuesta. Luego se buscaría otra, etc. Hay varios teoremas sobre el número de soluciones reales, sobre los límites inferior y superior de las respuestas, etc

Pero solo con la teoría matemática es muy pesado resolver estas ecuaciones. Se puede dibujar la gráfica con cualquier sencillo programa.

Los polinomios de grado 3,4 o 5 suelen tener pendientes muy elevadas, si quieres ver toda la altura se debe tomar mucho trozo en horizontal y no se ve por donde cortan al eje X. Esto se puede arreglar dividiendo el polinomio por una constante adecuada para hacer la gráfica. En concreto este lo dividí entre 5. Antes hice la gráfica más amplia para ver que no había raíces mas a la derecha o a la izquierda.

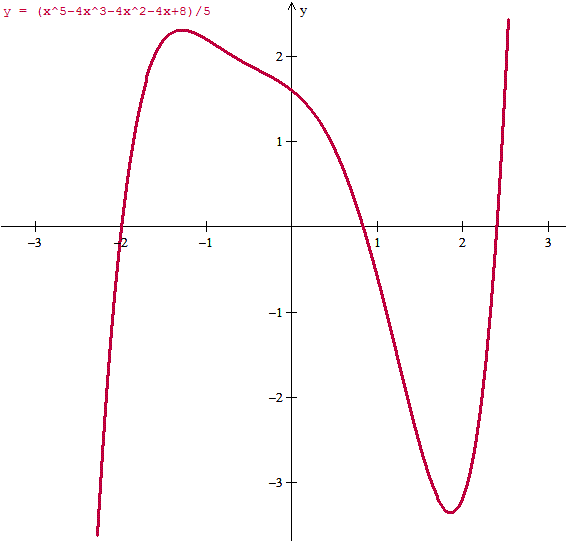
Y esos puntos de corte que se adivinan pueden servir como aproximación inicial en el método de Newton.

Pero si lo único que te interesa es conocer las soluciones puedes usar algún programa matemático. El más famoso es Mathlab, pero como a mi no me gusta porque es inmenso utilizo otro llamado Máxima que ademas es libre. Si escribo la orden

allroots(x^5 - 4*x^3 - 4*x^2 - 4*x + 8);

me da los resultados

[x=0.83188261099247,

x=1.272019649514069*%i-0.61803398874989,

x=-1.272019649514069*%i-0.61803398874989,

x=-2.0,

x=2.404185366507318]

Y sin ningún programa, puedes usar la página de WolframAlpha

Y allí escribes x^5 - 4x^3 - 4x^2 - 4x + 8