Las diagonales de un trapecio no se bisecan entre sí.

Vamos a demostrar que la proporción entre los segmentos en que se corta cada diagonal es la proporción que hay entre las bases. Entonces los dos trozos serían iguales si lo fueran las bases. Pero es que entonces ya no sería un trapecio, sería un rectángulo o un trapecio.

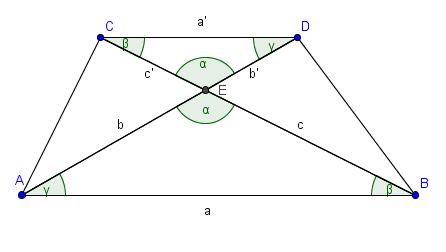
Por ser los triángulos ABE y DCE opuestos por el vértice E con los lados opuestos AB y DC paralelos son triángulos semejantes. En el dibujo están marcados los ángulos congruentes con la misma letra griega y los lados correspondientes con la misma letra y una prima en los lados de DCE.

Por el Teorema de Thales para triángulos semejantes tenemos

a/a' = b/b' = c'/c'

Asi los segmentos en que se corta la diagonal primera son

b/b' = a/a'

Si fueran iguales b y b' lo serían a y a' y no sería un trapecio como decía.

EL mismo argumento sirve par la otra diagonal.

Y eso es todo.