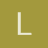Ecuación de Bernoulli dy/dx+y=1/y^1/2
me podrían ayudar a resolver una ecuación de Bernoulli; inicialmente me dan y^1/2dy/dx+y^3/2=1 de esto yo llego a dy/dx+y=1/y^1/2 pero empiezo a resolverla y no soy capaz de terminar.
1 Respuesta
Lo primero es quitar el y^(-1/2) del miembro derecho, es decir, para ello multiplicamos toda la ecuación por y^(1/2) y queda lo que nos daban:
y^(1/2)dy/dx + y^(3/2) = 1
Hacemos la sustitución
z=y^(3/2)
dz/dx = (3/2)y^(1/2) dy/dx ==> y^(1/2)dy/dx = (2/3)dz/dx
con lo que la ecuación queda en
(2/3)dz/dx + z = 1
(2/3)dz/dx = 1-z
(2/3)dz = (1-z)dx
(2/3)dz/(1-z) = dx
Es una ecuación de variables separadas que integramos a cada lado y queda
(2/3) ln(1-z) = x
ln(1-z) = (3/2)x
Cuando hay logaritmos neperianos se usa el truco de poner la constante como ln C en lugar de C
vamos a ponerla ya
ln(1-z) + ln C = 3x/2
ln[C(1-z)] = 3x/2
Cambiamos z por su valor
ln [C(1-y^(3/2))] = 3x/2
Aplicamos la función inversa que es e^x
C[1-y^(3/2)] = e^(3x/2)
1-y^(3/2) = e^(3x/2) / C
Siempre se puede retocar la constante sobre la marcha para que moleste lo menos posible, supondremos que inicialmente era ln(1/C) y ahora podremos poner
1-y^(3/2) = Ce^(3x/2)
y^(3/2) =1- Ce^(3x/2)
y = [1 - Ce^(3x/2)]^(2/3)
Y eso es todo.
Tu procedimiento esta muy claro, pero no se supone que la ecuación de bernoulli yo la debo de convertir en una ecuación diferencial lineal y de ahi resolverla hallando el factor integrante??
Si, eso es lo que sucede normalmente.
La ecuación de Bernoulli es
dy/dx + P(x)·y = Q(x)·y^n
y tras el cambio queda
dz/dx +(-n+1)P(x)·z = (-n+1)Q(x)
que es una ecuación diferencial lineal.
Pero es que este ejercicio es muy sencillo porque P(x)=Q(x)=1 y lo que queda es
dz/dx + (1/2 +1)·1·z =(1/2+1)·1
dz/dx + (3/2)z = 3/2
Que es equivalente a lo que calculé antes aunque parezca distinto. Y se pueden separar las variables sin tener que hacer los complejos cálculos de las ecuaciones lineales serias.
dz/dx = (3/2)(1-z)
dz/(1-z) = (3/2)dx
Y se integra y sale lo mismo que antes.
Eso es todo.
