El problema dice hallar la masa de la superficie esférica, se han debido equivocar, una superficie no tiene masa, tiene masa el sólido limitado por unas superficies.
La esfera no tiene problema es una esfera centrada en el origen de radio 2.
El cilindro es vertical ya que no aparece la z, su proyección sobre el plano xy es una lemniscata.
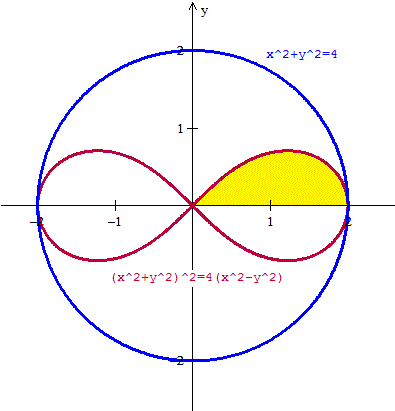
En amarillo está la proyección de la figura sobre el plano z=0
Pues esto parece que se tenga que integrar con coordenadas cilíndricas pero primero la ponemos con coordenadas cartesianas
$$\begin{align}&m=\iiint_F\gamma(x,y,z)dV=\\ &\\ &=\iiint_F (2x^2+2y^2+z^2+4)dz\,dy\,dx\\ &\\ &\end{align}$$No pongo los límites en cartesianas porque es muy difícil, mientras que con el cambio a cilindricas van a quedar límiters razonables espero.
El cambio a cilíndricas es
$$\begin{align}&x=\rho \cos\theta\\ &y=\rho sen\theta\\ &z=z\\ &Jacobiano= \rho\end{align}$$Necesitamos conocer el límite del ángulo theta. Para ello pasamos a polares la ecuación de la lemniscata
$$\begin{align}&(x^2+y^2)^2=4(x^2-y^2)\\ &(\rho^2cos^2 \theta+\rho^2sen^2\theta)^2=4(\rho^2cos^2 \theta-\rho^2sen^2\theta)\\ &(\rho^2)^2=4\rho^2(\cos^2\theta-sen^2\theta)\\ &\rho^2 = 4cos(2\theta)\end{align}$$El ángulo theta necesario para barrer la figura amarilla empieza en 0 y termina cuando el radio vector es cero
0 = 4cos(2theta)
cos(2theta) = 0
2theta = pi/2
theta = pi/4
Luego el dominio en rho y theta de la leminiscata es
rho € [0, 4cos(2theta)]
theta € [0, pi/4]
y el dominio en z esta entre 0 y la altura de la esfera
z = sqrt(4-x^2-y^2) = sqrt[4 -(x^2+y^2)] = sqrt(4 - rho^2)
z € [0, sqrt(4 - rho^2)]
finalmente el cambio de variable para la densidad será
gamma(x,y,z) = 2x^2+2y^2+z^2-4 = 2rho^2+z^2 -4
y no hay que olvidar que hay que multiplicar por el jacobiano que era rho
Con todo esto la integral en cilíndricas queda
$$\begin{align}&m=\int_0^{\pi/4}\int_0^{4cos(2/\theta)}\int_0^{\sqrt{4-\rho^2}}\rho(2\rho^2+z^2-4)dz\,d\rho\,d\theta=\\ &\\ &\int_0^{\pi/4}\int_0^{4cos(2\theta)}\left[\rho(2\rho^2-4)z+\rho \frac{z^3}{3} \right]_0^{\sqrt{4-\rho^2}}d\rho\,d\theta=\\ &\\ &\end{align}$$Nada, no vamos a seguir, ya he comprobado con el ordenador que eso no se puede integrar.
Y sin hacer el cambio va a ser peor pero probamos.
Tendremos que poner la lemniscata como función de x
$$\begin{align}&(x^2+y^2)^2=4(x^2-y^2)\\ &x^4+y^4+2x^2y^2 = 4x^2-4y^2\\ &y^4+(2x^2+4)y^2+x^4-4x^2=0\\ &\\ &y^2=\frac{-2x^2-4\pm \sqrt{(2x^2+4)^2-4x^4+16x^2}}{2}=\\ &\\ &\frac{-2x^2-4\pm \sqrt{4x^4+16+16x^2-4x^4+16x^2}}{2}=\\ &\\ &-x^2-2\pm 2 \sqrt{1+2x^2}\\ &\\ &y=\pm \sqrt{-x^2-2\pm 2 \sqrt{1+2x^2}}\\ &\\ &\text{nos interesa que sea real y positiva}\\ &\\ &y=\sqrt{-x^2-2+ 2 \sqrt{1+2x^2}}\end{align}$$Y vamos a ver que engendro queda
$$\begin{align}&V=\int_0^2\int_0^{\sqrt{-x^2-2+ 2 \sqrt{1+2x^2}}}\int_0^{\sqrt{4-x^2-y^2}}(2x^2+2y^2+z^2-4)dzdydx=\\ &\\ &\int_0^2\int_0^{\sqrt{-x^2-2+ 2 \sqrt{1+2x^2}}}\left[(2x^2+2y^2-4)z+\frac{z^3}{3}\right]_0^{\sqrt{4-x^2-y^2}}dydx=\\ &\end{align}$$Y por aquí tampoco vamos a llegar a ningún sitio.
El problema es muy complicado o ha habido algún fallo en el enunciado. ¿De dónde ha salido?


