La clave es demostrar las fórmulas para la suma/resta de ángulos
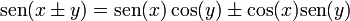
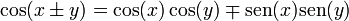
En el siguiente enlace puedes encontrar la demostración
http://www.sectormatematica.cl/proyectos/suma_y_diferencia.htmUna vez demostrado estas dos fórmulas, para expresar sen 2theta y cos 2theta en función de theta tan solo tienes que sustituir x= theta e y = theta en las fórmulas del seno y coseno de la suma. Así, te quedará
sen(2theta) = 2sen(theta)cos(theta)
cos(2theta) = cos(theta)^2 - sen(theta)^2
Para expresar sen alpha - sen beta en términos de (alpha+beta/2) y (alpha-beta/2)
necesitamos primero demostrar esta fórmula
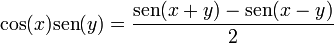
que se obtiene de escribir por separado la fórmula
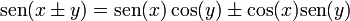
y restarlas. Es decir:
sen(x+y) = sen(x)cos(y) + cos(x)sen(y)
sen(x-y) = sen(x)cos(y) - cos(x)sen(y)
ahora restamos:
sen(x+y) - sen(x-y) = 2cos(x)sen(y)
y dividiendo la igualdad entre 2 tenemos
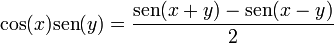
Finalmente tan solo queda sustituir x= (alpha + beta)/2 e y=(alpha - beta)/2 quedando
2cos((alpha + beta)/2) sen((alpha - beta)/2) = sen(alpha) - sen(beta)
Que es lo que queríamos demostrar.
En esta página explican bastantes cosas de las identidades trigonométricas:
http://es.wikipedia.org/wiki/Identidades_trigonom%C3%A9tricas


