Eliminar término xy de la curva trazar su lugar geométrico y ambos sistemas de ejes coordenado
1. Por una rotación de coordenadas, elimina el término xy de la curva
$$2x^2+\sqrt{3xy}+y^2=4$$traza su lugar geométrico y ambos sistemas de ejes coordenados. (Sugerencia: Sustituye las ecuaciones de rotación y resuelve para el ángulo
$${\zeta}$$de tal forma que el coeficiente del término xy se vuelva cero).
1 Respuesta
El ejercicio se hace exactamente igual que el que ya hice la otra vez, la diferencia entre en el 4 y el 9 que había únicamente afecta al tamaño de la elipse, pero el ángulo de los ejes de la elipse y el centro son los mismos y con el mismo giro se elimina el término en xy.
La ecuación que da las coordenadas viejas (x.y) A partir de las nuevas (z, t) es:
x = zcosa - tsena
y = zsena + tcosa
2x^2 + sqrt(3)xy + y^2 = 4
2(z·cosa - t·sena)^2 + sqrt(3)(z·cosa - t·sena)(z·sena + t·cosa) + (z·sena + t·cosa)^2 =9
2[z^2·cos^2a + t^2·sen^2(a) - 2zt·cosa·sena] +
sqrt(3)[z^2·cosa·sena + zt·cos^2(a) - tz·sen^2(a) - t^2sena·cosa) +
z^2·sen^2(a) + t^2·cos^2(a) + 2zt·sena·cosa = 4
Solo nos interesa dejar a cero la suma de términos que contienen zt
-4cosa·sena + sqrt(3)·[cos^2(a)-sen^2(a)] + 2sena·cosa=
-2sena·cosa + sqrt(3)·[cos^2(a)-sen^2(a)] =
-sen(2a) + sqrt(3)·cos(2a) = 0
-sqrt[1 - cos^2(2a) + sqrt(3)cos(2a)=0
-sqrt[1 - cos^2(2a)] = - sqrt(3)cos(2a)
Elevamos al cuadrado
1 - cos^2(2a) = 3cos^2(2a)
4cos^2(2a) =1
cos^2(2a) = 1/4
cos(2a) = +- 1/2
2a = pi/3, 2pi/3, 4pi/3, 5pi/3, 7pi/3, 8pi/3, 10pi/3, 11pi/3
a = pi/6, pi/3, 2pi/3, 5pi/6, 7pi/6, 4pi/3, 5pi/3, 11pi/6
Pero puede que alguna no sirva porque al elevar al cuadrado se introducen
soluciones fantasma.
Lo comprobamos con la ecuación
-sen(2a) + sqrt(3)·cos(2a) = 0
-sen(pi/3) + sqrt(3)·cos(pi/3) = -sen60º + sqrt(3)cos60º = -sqrt(3)/2 + sqrt(3)(1/2) = 0
-sen(2pi/3) + sqrt(3)cos(2pi/3) = -sen120º+ sqrt(3)cos120º = -sqrt(3)/2 - sqrt(3)(1/2)
-sen(4pi/3) + sqrt(3)cos(2pi/3) = -sen240º+ sqrt(3)cos240º = sqrt(3)/2 - sqrt(3)(1/2) = 0
-sen(5pi/3) + sqrt(3)·cos(5pi/3) = -sen300º + sqrt(3)cos300º = sqrt(3)/2 +sqrt(3)·(1/2)
...
siguiendo se comprueba que valen 8pi/3 y 11pi/3
Luego los ángulos validos son 2a=pi/3, 4pi/3, 7pi/3 y 10pi/3
a=pi/6, 2pi/3, 7pi/6 y 5pi/3 = 30º, 120º, 210º y 300º
Esta es la gráfica:
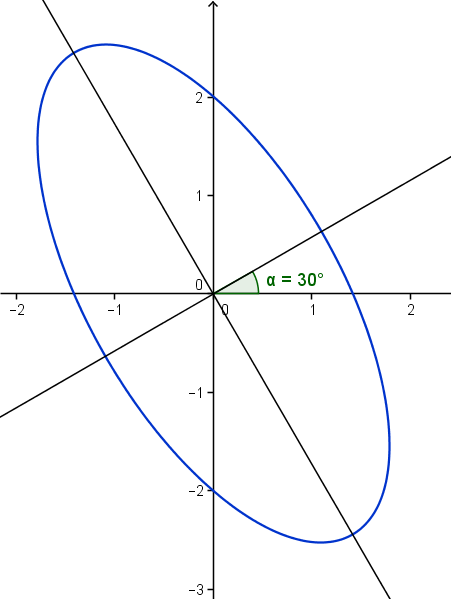
Ahi ase ve que girando 30º los ejes por ejemplo los ejes de la elipse son X e Y
Y eso es todo.
