Hallar la ecuación de la recta tangente a la función en el punto .
Hallar la ecuación de la recta tangente a la función xy^2 - 4x^3y + x/y + 2 = 0 en el punto (1,1).
1 Respuesta
Cuando hay una / en una expresión es conveniente usar los paréntesis para delimitar el numerador y denominador pues el que no ha visto la expresión original no sabe donde empieza uno ni donde termina el otro.
Confírmame cual de estas dos expresiones es, u otra.
$$\begin{align}&1)\quad xy^2 - 4x^3y + \frac xy + 2 = 0\\ &\\ &2)\quad \frac{xy^2 - 4x^3y + x}{y + 2} = 0\end{align}$$Espero la respuesta, ojala sea la 1)
Oh! perdón, por la omisión, pero si, efectivamente es la opción uno.
Saludos.
Para hallar la recta tangente se usa la fórmula
y = yo + f '(xo)(x-xo)
El punto (xo,yo) es (1, 1). Lo único que nos falta es calcular f '(xo). LO haremos por derivación implícita.
$$\begin{align}&xy^2 - 4x^3y + \frac xy + 2 = 0\\ &\\ &y^2 + 2xyy' - 12x^2y - 4x^3y' + \frac{y-xy'}{y^2} = 0\\ &\\ &y^4+2xy^3y'-12x^2y^3-4x^3y^2y'+y-xy'=0\\ &\\ &2xy^3y'-4x^3y^2y'-xy'=-y^4+12x^2y^3-y\\ &\\ &y'=\frac{-y^4+12x^2y^3-y}{2xy^3-4x^3y^2-x}\\ &\\ &\\ &\text{La derivada en (1,1) es}\\ &\\ &f'(1)=\frac{-1+12-1}{2-4-1}= \frac{10}{-3}= - \frac{10}{3}\\ &\\ &\text {Y la tangente será}\\ &\\ &y = 1 -\frac{10}{3}(x-1)\\ &\\ &y = -\frac{10x}{3}+\frac{13}{3}\end{align}$$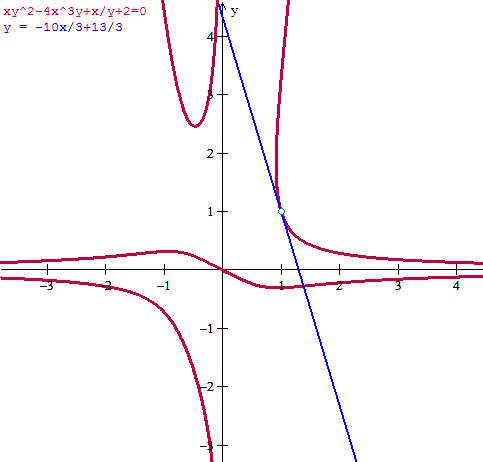
La gráfica permite suponer que el resultado está bien aunque no sea siempre cierto, rectas muy parecidas podrían parecer también la tangente.
Y eso es todo.
y si Por definición, la recta tangente está dada por :Y= f´(x0)(x-x0)+f(x0)? - Raul Swetter