Determina la ecuación en su forma elíptica
Considera las siguientes dimensiones del techo del edificio del Capitolio en Washington y resuelve lo que se te indica.
-Eje mayor: 180 metros
-Eje menor: 90 metros
-Supón que el eje focal se encuentra sobre el eje de las x.
a)Determina la ecuación de la forma elíptica del techo considerando su C (0, 0).
b) Obtén todos los elementos que componen a la forma elíptica del techo.
c)Convierte a su forma general la ecuación ordinaria que obtuviste en el inciso a.
d)Determina la ecuación general de la forma elíptica del techo suponiendo que el
Centro está en C (12, –9).
e) A partir de la forma general de la ecuación de la elipse que obtuviste en elinciso d, obtén la ecuación en su forma ordinaria.
f) Traza sobre un plano cartesiano la elipse con sus elementos distinguiéndolos con
Colores diferentes.
2 respuestas
Este problema me recordaba tremendamente al del estadio Azteca, he visto que lo mandaste tú también.
a) Para obtener la ecuación canónica de una elipse es necesario conocer los semiejes, el centro y el eje longitudinal. O focal. Los semiejes son
a = Semieje mayor = 180/2 = 90
b = Semieje menor = 90/2 = 45
El semieje mayor ira al denominador del eje focal en la ecuación, es decir debajo de la x
$$\begin{align}&\frac{(x-x_0)^2}{a^2}+\frac{(y-y_0)^2}{b^2}=1\\ &\\ &siendo\: (x_0,y_0)\;el\; centro\\ &\\ &\text{La ecuación canónica u ordinaria es:}\\ &\\ &\frac{x^2}{90^2}+\frac{y^2}{45^2}=1\end{align}$$b) Para conocer otros datos es preciso calcular la semidistancia focal que se llama c y es la mitad de la distancia entre focos. Y se calcula así
$$\begin{align}&c=\sqrt{a^2-b^2}= \sqrt{90^2-45^2}=\\ &\\ &\sqrt{8100-2025}=\sqrt{6075} =45 \sqrt 3\end{align}$$Los focos estarán a esa distancia del centro sobe el eje X, uno a cada lado-
Los elementos son estos
Eje mayor que es la distancia: 2a = 190 m
Semieje mayo: a = 90 m
Semieje menor: b = 45 m
Semidistancia focal: c: = 45sqrt(3) = 77.94228634 m
Eje focal o longitudinal: Eje X
Focos (-45sqrt(3), 0) y ( 45sqrt(3), 0) o en decimal
(-77.94228634, 0) y (77.94228634, 0)
c)
$$\begin{align}&\frac{x^2}{90^2}+\frac{y^2}{45^2}=1\\ &\\ &\frac{45^2x^2+90^2y^2}{90^245^2}=1\\ &\\ &45^2x^2+90^2y^2 = 90^245^2\\ &\\ &\text{Dividimos por }45^2\\ &\\ &x^2 +4y2 = 90^2\\ &x^2+4y^2-8100=0\end{align}$$d) C(12,-9)
Si a los puntos (x, y) de la elipse nueva les restamos (12,-9) tendremos los de la vieja que cumplen la ecuación que calculamos antes
$$\begin{align}&(x-12)^2+4(y+9)^2-8100=0\\ &\\ &x^2-24x+144+4y^2+72y+324-8100=0\\ &\\ &x^2+4y^2-24x+72y -7632=0\end{align}$$e) Este ejercicio es tonto. La ecuación ordinaria nueva se obtiene a prtit de la ordinaria vieja, pero vamos a hacerlo como si no hubieramos hecho nada antes y nos dieran esa ecuación general. Hay que completar cuadrados para elíminar los términos que tienen solo la x e y.
$$\begin{align}&x^2+4y^2-24x+72y -7632=0\\ &\\ &(x-12)^2 = x^2-24x+144 \implies x^2-24x = (x-12)^2-144\\ &\\ &4(y+9)^2=4y^2+72x +324\implies4y^2+72x=4(y+9)^2-324\\ &\\ &\text{Sustituímos esto en la ecuación}\\ &\\ &(x-12)^2-144+4(y+9)^2-324-7632=0\\ &\\ &(x-12)^2+4(y+9)^2-8100=0\\ &\\ &(x-12)^2+4(y+9)^2=8100\\ &\\ &\frac{(x-12)^2}{8100}+\frac{4(y+9)^2}{8100}=1\\ &\\ &\frac{(x-12)^2}{90^2}+\frac{(y+9)^2}{2025}=1\\ &\\ &\frac{(x-12)^2}{90^2}+\frac{(y+9)^2}{45^2}=1\\ &\end{align}$$f) Esta es la gráfica de la elipse.
Y eso es todo.
muchas gracias
Fue para simplificar la ecuación
$$\begin{align}&45^2x^2+90^2y^2 = 90^245^2\\ &\\ &\text{Dividimos por }45^2\\ &\\ &x^2 +4y2 = 90^2\\ &x^2+4y^2-8100=0\end{align}$$Puedes hacer la cuenta si quieres
90^2 = 8100
45^2 = 2025
8100/2025 = 4
Pero yo lo hice de una forma más inmediata mentalmente, estos son los pasos pero si se escriben pierde la gracia, hay que hacerlos mentalmente
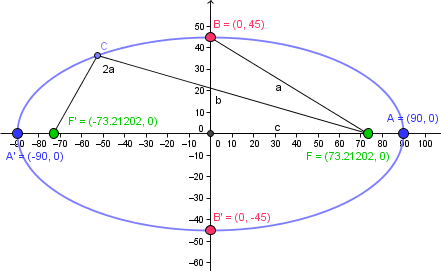
$$\begin{align}&\frac{90^2}{45^2}= \frac{(2·45)^2}{45^2}=\frac{2^2·45^2}{45^2}=2^2=4\end{align}$$Y eso es todo.
Como obtuviste 4y^2 del inciso C? se que diviste entre 45 , pero quiero saber el porque? - Cintia Luna