Considera las siguientes dimensiones del techo del edificio del Capitolio en Washington y resuelve l

a) Para obtener la ecuación canónica de una elipse es necesario conocer los semiejes, el centro y el eje longitudinal. o focal. Los semiejes son
a = Semieje mayor = 180/2 = 90
b = Semieje menor = 90/2 = 45
El semieje mayor ira al denominador del eje focal en la ecuación, es decir debajo de la x

$$\begin{align}&\frac{(x-x_0)^2}{a^2}+\frac{(y-y_0)^2}{b^2}=1\\ &\\ &siendo\: (x_0,y_0)\;el\; centro\\ &\\ &\text{La ecuación canónica u ordinaria es:}\\ &\\ &\frac{x^2}{90^2}+\frac{y^2}{45^2}=1\end{align}$$

b) Para conocer otros datos es preciso calcular la semidistancia focal que se llama c y es la mitad de la distancia entre focos. Y se calcula así

$$\begin{align}&c=\sqrt{a^2-b^2}= \sqrt{90^2-45^2}=\\ &\\ &\sqrt{8100-2025}=\sqrt{6075} =45 \sqrt 3\end{align}$$

Los focos estarán a esa distancia del centro sobe el eje X, uno a cada lado.
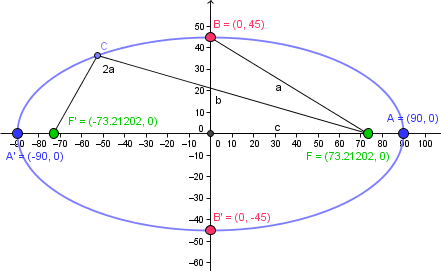
Los elementos son estos
Eje mayor que es la distancia: 2a = 190 m
Semieje mayo: a = 90 m
Semieje menor: b = 45 m
Semidistancia focal: c: = 45sqrt(3) = 77.94228634 m
Eje focal o longitudinal: Eje X
Focos (-45sqrt(3), 0) y ( 45sqrt(3), 0) o en decimal
(-77.94228634, 0) y (77.94228634, 0)

c)

$$\begin{align}&\frac{x^2}{90^2}+\frac{y^2}{45^2}=1\\ &\\ &\frac{45^2x^2+90^2y^2}{90^245^2}=1\\ &\\ &45^2x^2+90^2y^2 = 90^245^2\\ &\\ &\text{Dividimos por }45^2\\ &\\ &x^2 +4y2 = 90^2\\ &x^2+4y^2-8100=0\end{align}$$

d) C(12,-9)
Si a los puntos (x, y) de la elipse nueva les restamos (12,-9) tendremos los de la vieja que cumplen la ecuación que calculamos antes

$$\begin{align}&(x-12)^2+4(y+9)^2-8100=0\\ &\\ &x^2-24x+144+4y^2+72y+324-8100=0\\ &\\ &x^2+4y^2-24x+72y -7632=0\end{align}$$

e) Este ejercicio es tonto. La ecuación ordinaria nueva se obtiene a partir de la ordinaria vieja, pero vamos a hacerlo como si no hubiéramos hecho nada antes y nos dieran esa ecuación general. Hay que completar cuadrados para eliminar los términos que tienen solo la x e y.

$$\begin{align}&x^2+4y^2-24x+72y -7632=0\\ &\\ &(x-12)^2 = x^2-24x+144 \implies x^2-24x = (x-12)^2-144\\ &\\ &4(y+9)^2=4y^2+72x +324\implies4y^2+72x=4(y+9)^2-324\\ &\\ &\text{Sustituímos esto en la ecuación}\\ &\\ &(x-12)^2-144+4(y+9)^2-324-7632=0\\ &\\ &(x-12)^2+4(y+9)^2-8100=0\\ &\\ &(x-12)^2+4(y+9)^2=8100\\ &\\ &\frac{(x-12)^2}{8100}+\frac{4(y+9)^2}{8100}=1\\ &\\ &\frac{(x-12)^2}{90^2}+\frac{(y+9)^2}{2025}=1\\ &\\ &\frac{(x-12)^2}{90^2}+\frac{(y+9)^2}{45^2}=1\\ &\end{align}$$

f)f) Esta es la gráfica de la elipse.

hola

me podrían decir como ver lsa ecuaciones de las respuestas por favor urgente gracias

saludos