Raíces de ecuciones no lineales

Aquí sería muy conveniente saber qué método has estudiado para este cálculo. Nueve decimales no se piden todos los días, incluso muchas calculadoras ni siquiera los tienen.

Incluso no sé si te dejarían usar el ordenador.

Bueno, vamos a intentarlo por el método de la cuerda. Dividiremos cada vez el intervalo en dos artes de modo que en los extremos haya signo distinto

h(0) = -1

h(2) = 0,81...

h(1) =-0,15

Tomamos el intervalo [1,2] el punto intermedio es 1,5

h(1,5) = 0,49...

Tomamos [1, 1.5] el punto intermedio es 1,25

h(1,25) = 0,18..

Tomamos [1, 1.25] el punto intermedio es1,125

h(1,125)=0,015

Tomamos [1, 1.125] el punto intermedio es 1,0625

h(1,0625)=-0,071..

Tomamos [1.0625, 1.125] el punto intermedio es 1,09375

h(1.09375) = -0,028...

Tomamos [1.09375, 1.125] el punto intermedio es 1.109375

h(1,109375) = -0,0066

Tomamos [1.109375, 1,125] el punto intermedio es 1.1171875

h(1.1171875) =0,0042...

Tomamos [1.109375, 1.1171875] el punto intermedio es 1.11328125

h(1.11328125) =-0,00121

Bueno, ya puedes ver que la convergencia es extremadamente lenta para hacerlo a mano, aun nos quedaría mucho.

-------------------------------------------------------------------------------------------------

Veremos con el método de Newton-Fourier.

En este método debe haber un solo cero de h entre los extremos a y b; y que h' y h'' no se anulen en el intervalo.

Entonces se toma el extremo de los dos, llamémoslo m donde signo h = signo h''

El valor c=m-h(m)/h'(m) es mejor aproximación que m a la raíz

Y una cota del error es k(b-a)^2/(2|h'(m)|) donde k es una cota superior de |h''(x)| en el intervalo (a, b)

Es un método más complicado y a primera vista puede parecer que peor que el anterior pero solo en el comienzo. Se puede aproximar inicialmente algo con el método de la cuerda y luego usar este.

Veamos que se cumplen las condiciones.

h(x) = x·senx-1

He hecho la gráfica y visto que solo hay un cero en [0,2]

Las derivadas son:

h'(x) = senx+xcosx

h''(x) = cosx+ cosx -xsenx = 2cosx - xsenx

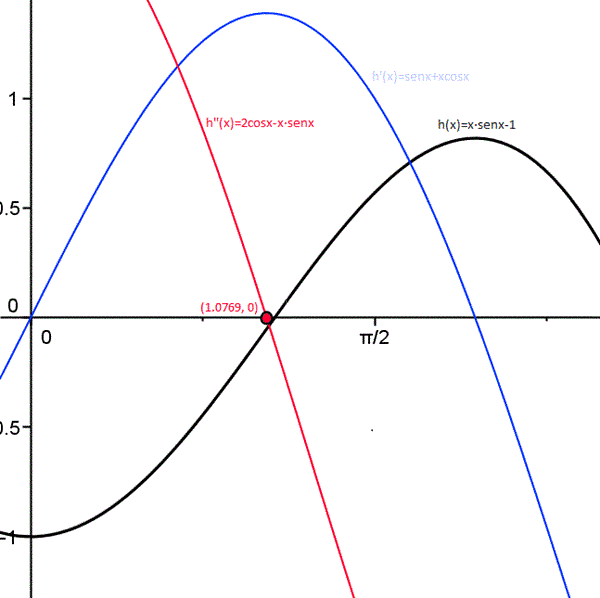
Vemos que hay que afinar en el intervalo para garantizar que la derivada segunda (en rojo) no cambie de signo. El extremo izquierdo debe ser mayor que 1,0769. Pues lo mejor será lo que he dicho. Tomemos como punto de partida lo realizado hasta ahora con el método de la cuerda.

Tomaremos como intervalo inicial:

[1.11328125, 1.1171875]

Ahí queda garantizado que la derivada segunda es siempre negativa.

Tomamos el extremo m con igual signo que la derivada segunda, es el izquierdo, donde h(x) es negativa. Y apliquemos las iteraciones:

c = m - h(m) / h'(m)

con m = 1,11328125

c = m - (m·senm -1)/(senm+xcosm) = 1.114157109

Tomamos m =1.114157109 y operamos de nuevo. Nos da

1.114157141

Operamos de nuevo con ese valor y nos da el mismo

1.114157141

Luego ese es el valor.

Vamos a calcular

h(1.114157141) = 0

La calculadora de 10 dígitos que tengo no aprecia error en la respuesta dada. Lo que pasa es que se guardaba decimales internos que no me quiere enseñar. Espera que hago la operación escribiendo a mano los decimales

h(1.114157141) = 1.7786 ·10^(-10)

Es más que suficiente para lo que nos pedían.

Pero vamos a hacerlo requetebién ya que nos hemos puesto. Hacemos las cuentas con Máxima, un programa de ordenador que tiene más decimales de precisión.

Se empieza con una orden

x:1.11328125;

y luego las iteraciones se hacen con

x:x-(x*sin(x)-1)/(sin(x)+x*cos(x));

Y nos va dando

1.1141571087595

1.11415714087193

1.11415714087193

Y ya no mejora, luego esa es la respuesta. Hay programas con más precisión todavía como Scilab o calculadoras con hasta 90 dígitos, pero hemos cumplido de sobra lo que nos pedían.

Y yo me quedo con la intriga de qué método usáis vosotros en vuestro libro o apuntes. Dímelo