Como resuelvo este ejercicio de geometría analitica?
Sea ABCD un trapecio birrectángulo (ángulos DAB y ABC rectos) que cumple: A(8,1), los vértices B y D tienen ordenada 4, la ecuación de la recta AB es x-2y-6=0 y el angulo ABC = 45°. Hallar las coordenadas de sus vértices.
No lo entiendo, no se como hacer!! Les agradecería mucho su ayuda!!! :)
1 respuesta
Hola! tu sabes que asi esta escrito en el ejercicio que me paso el profesor. Yo no lo entiendo, pero quizá el angulo de 45° sea BCD? o no es posible? gracias por tu tiempo!!
Sí, si hacemos que los 45º sean los del angulo BCD queda todo bien. La otra posibilidad de que fuera el águlo ADC hacia que la figura no fuera un trapecio sino una mariposa.
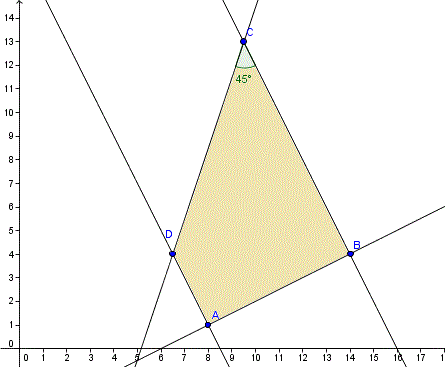
Tenemos la recta AB
x-2y-6=0
Sobre ella está el punto A(8,1)
El punto B es el que tiene ordenada 4, luego:
x - 2·4 - 6 = 0
x -8 -6 = 0
x=14
Luego B(14,4)
La recta perpendicular pasando por A nos dará el punto D
El vector de la recta AB es (2,1)
porque en una recta de la forma
ax+by+c=0
el vector director es (b, -a) o (-b, a)
El vector perpendicular es (1, -2)
porque el producto escalar será
(2, 1)·(1, -2) = 2·1 - 1·2 = 0
La recta AD es ls perpendicular pasando por A es
(x-8) / 1 = (y-1)/(-2)
-2x+16 = y-1
2x+y-17=0
Y si D tiene ordenada 4 es
2x+4-17 = 0
2x = 13
x = 13/2
Luego D(13/2, 4)
Y ahora queda lo complicado
C estará sobre la recta perpendicular a AB que pasa por B(14,4)
Su vector ya lo calculamos, es (1, -2) Y la ecuación de la recta será
(x-14)/1 = (y-4)/(-2)
-2x+28 = y-4
2x+y-32 =0
Ahora debemos hallar la recta que forma 45º con esta y pasa por el punto D
Primero hay que hallar la pendiente de la recta CD.
Tenemos que BC tiene vector proporcional a (-1, 2) que es paralelo al que calculabamos para la recta AD. Y el vector CD tendrá 135º más.
Por fórmulas trigonométricas
tg(a+b) = (tga + tgb) / (1 - tga·tgb)
tg(a+135) = (tga-1) / (1 + tga)
como tga=2/(-1) = -2
tg(a+135)=-3/-1 = 3
La tangente es el cociente de la componete y del vector entre la componente x.
Luego el vector de CD es (1,3) o (-1,-3)
Y la recta pasando con ese vector pasando por D es
(x - 13/2) / 1 = (y-4) / 3
3x - 39/2 = y-4
3x - y - 31/2 = 0
Ya solo queda calcular la intersección de esta recta con la BC, que ahora que lo veo aun no se calculó.
Por ser paralela a AD tiene la forma
2x+y + c = 0
por pasar por (14,4)
28+4+c = 0
c=-32
Luego la recta BC es
2x+y-32=0
y calculamos la intersección con
3x-y-31/2=0
Las sumamos
5x -95/2 = 0
x = 19/2
y = 32-2x = 32-19 = 13
Luego C(19/2, 13)
Y eso es todo, espero que te sirva y lo hayas entendido. No sé si lo que he empleado de la suma de tangentes sobrepasa tus estudios, pero lo intenté hacer por que el producto escalar de dos vectores fuera el coseno de 45 y era dificilísimo.
De todas formas sé que hay una formula que te da la tangente del ángulo de dos rectas en función de las pendientes y es un método equivalente a lo que hice.
