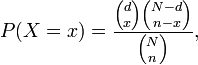Problema de distribución hipergeométrica

La distribución hipergeométrica tiene una fórmula que nunca te acuerdas de ella para toda la vida. Voy a buscarla.

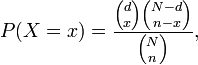
Donde N es el tamaño de población, n es el tamaño de la muestra extraída, d es el número de elementos en la población original que pertenecen a la categoría deseada y x es el número de elementos en la muestra que pertenecen a dicha categoría

Luego en nuestro ejercicio

N=20

n=3

d=6 (solteras)

a) x=3

$$\begin{align}&P(X=3)=\frac{\binom 63 \binom{20-6}{3-3}}{\binom{20}{3}}=\\ &  \\ &  \frac{\binom 63 \binom{14}{0}}{\binom{20}{3}}=\frac{\binom 63}{\binom{20}{3}}=\\ &  \\ &  \frac{\frac{6·5·4}{3·2·1}}{\frac{20·19·18}{3·2·1}}=\frac{6·5·4}{20·19·18}=\frac 1{19·3}=\frac 1{57}\approx\\ &\\ &0.01754385965\end{align}$$

b) x=0

$$\begin{align}&P(X=0)=\frac{\binom 60 \binom{20-6}{3-0}}{\binom{20}{3}}=\frac{ \binom{14}{3}}{\binom{20}{3}}=\\ & \\ & \frac{14·13·12}{20·19·18}=\frac {2184}{6840}=\frac{91}{285}\approx 0.3192982456\end{align}$$

Y eso es todo.

¡Gracias!