Problema de visualización de funciones continuas 1
Considera los siguientes espacios topológicos: una esfera y una dona (solo las superficies). Ambos tienen la topología que les hereda:
$$\begin{align}&R^3\end{align}$$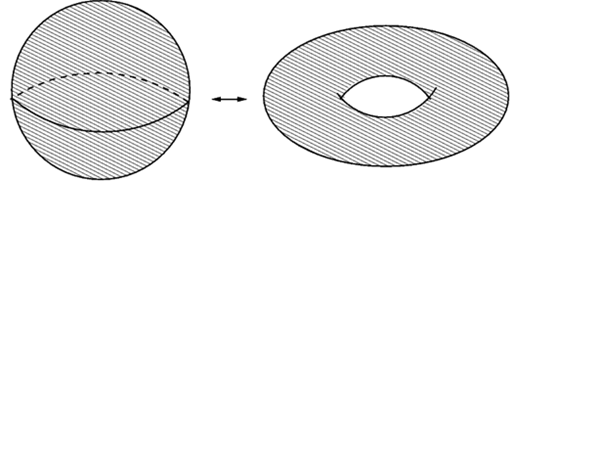
- Encuentra una función continua de la esfera a la dona. Describe la acción de la función que encontraste: ¿Cuál es su imagen? ¿Es inyectiva? ¿Es sobreyectiva? ¿Cuál es la imagen inversa de un abierto en la dona?
- Encuentra una función continua de la dona a la esfera. Describe la acción de la función que encontraste: ¿Cuál es su imagen? ¿Es inyectiva? ¿Es sobreyectiva? ¿Cuál es la imagen inversa de un abierto en la esfera?
- Escribe las razones por las que las funciones que encontraste son continuas.
Reflexiona: ¿Son homeomorfos los dos espacios? Escribe un argumento que justifique tu respuesta.
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
2

Hola, soy nuevo en este sitio; leí la pregunta de Amo Mo y sólo puedo responder que la esfera y el toro no son homeomorfos puesto que la esfera es simplemente conexa y el toro no lo es, i. e., al no conservarse la propiedad topológica entre ambos objetos, no existe homeomorfismo entre ellos. No obstante, no tengo mucha idea de las primeras 3 preguntas... ¿Quizá funciones constantes que mapeen de la esfera hacia el toro? ¿Me equivoco? - Gerjes Manuel Cosme
El hecho de que no sean homeomorfos no significa que no pueda haber una función continua de la esfera en el toro y viceversa. Puede haberlas pero sin inversa continua. Por ejemplo, hay una función continua, la obvia, del segmento [0,1) en una circunferencia pero la inversa no lo es. Saludos. - Valero Angel Serrano Mercadal