Hallar el ángulo entre los módulos de dos fuerzas
Acabo de comenzar la carrera de Ingeniero de materiales. Tengo un problem aue resolver y me he quedado bloqueado y no me dan los resultados. El problema es el siguiente. Alguien puede echarme una mano.
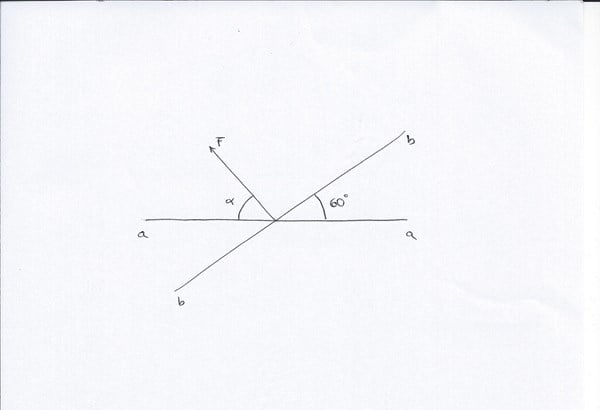
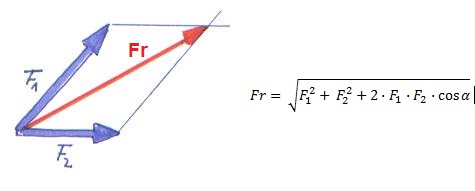
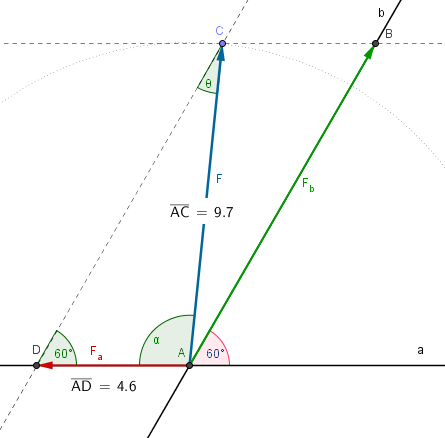
La fuerza 
de módulo 9.7kN debe descomponerse en sus componentes a lo largo de las líneas a-a y b-b. Determinar mediante construcción de triángulos el ángulo 
, en grados, si la componente de a lo largo de la línea a-a es igual a 4.6kN.
Ahttp://moodle.upm.es/titulaciones/oficiales/file.php/1885/Imagenes/01_FuerzaADescomponer.JPG
2 respuestas
Te adjunto la foto. Gracias
1º pasa líneas paralelas de ambas rectas y que pasen por el extremo del vector (por la punta de flecha)-
2º los puntos de intersección de la recta aa con bb, serán los vértices de los dos vectores descompuestos.
Y la ecuación general es:
... Donde en la raíz,,, alfa no es el de tu problema,,, es el que forma los vectores F1-F2, y le voy llamar af
Cuando el ángulo es obtuso en este caso, hay que tener cuidado,,, af = 180-60 = 120º
No es esa la respuesta. Pero para hacer la gráfica explicativa necesito que me digas si los 4.6 de la componente sobre la recta a son hacia la derecha o hacia la izquierda.
Lo normal sería hacia la derecha ya que es una cantidad positiva, pero según el dibujo que has hecho la componente sobre la recta a va a ser hacia la izquierda. Luego tendrás que decidirte por una de las dos posibilidades y lo resuelvo de acuerdo con ella.
Lo haré con el 4.6 hacia la izquierda que es lo que se asemeja más al dibujo.
Esta es la gráfica a escala real.
Tomemos el triangúlo ACD, le aplicaremos la ley de los senos
$$\begin{align}&\frac {sen\,\beta}{4.6}=\frac {sen\, 60º}{9.7}\\ &\\ &sen\beta=\frac{4.6}{9.7}·\frac{\sqrt 3}{2}\approx 0.4106924595\\ &\\ &\beta=arcsen(0.4106924595)=24.24834145º\\ &\\ &\alpha=180º-60º-24.24834145º=95.75165855º\end{align}$$