¿Como operar este otro caso de limites notables?

Lucho. Comienzo por presentarte a la función en estudio:

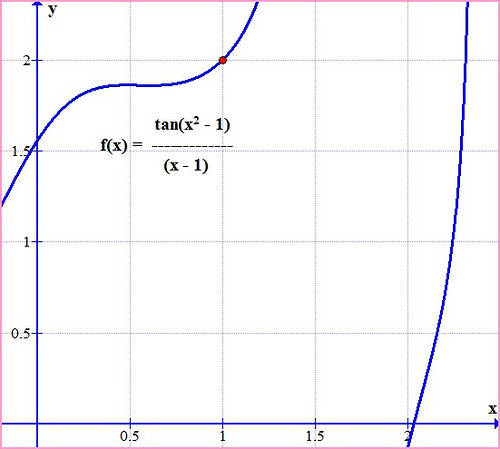
Convengamos que es una función "rarita" (por aquello de la periodicidad de la función tangente), pero -y lo importante es que- vemos que en las cercanías de "x = 1", la función tiende a "2"... ¡Vamos a demostrarlo!
Tienes que conocer dos conceptos:
a) Comencemos con uno de los límites más famosos:

$$\begin{align}&\lim_{z \to 0} \frac{sen(z)}{z}=1\end{align}$$

He utilizado la variable "z" pues estoy simbolizando (y resaltando) que "z" es -al mismo tiempo- el ángulo de la función seno y el divisor de la expresión. Por favor: ¡No pierdas jamás de vista esos dos detalles!
b) Y ahora recuerda uno de los productos más famosos:

$$\begin{align}&(z+1)(z-1)=z^2-1\end{align}$$

de donde deducimos muy fácilmente:

$$\begin{align}&z+1=\frac{(z^2-1)}{(z-1)}\end{align}$$

¿Ok?...
Entonces, y teniendo en cuenta estos dos resultados, analizaremos el límite:

$$\begin{align}&\lim_{x \to 1}\frac{tan(x^2-1}{(x-1)}\end{align}$$

Seguro que recuerdas que la función tangente puede expresarse como el cociente entre la función seno y la función coseno del mismo ángulo. Por lo tanto, lo anterior podemos ponerlo así:

$$\begin{align}&\frac{tan(x^2-1}{(x-1)}=sen(x^2-1)*\frac{1}{\cos(x^2 - 1)}*\frac{1}{(x-1)}\end{align}$$

$$\begin{align}&\frac{tan(x^2-1}{(x-1)}=\frac{sen(x^2-1)}{(x^2-1)}*\frac{1}{\cos(x^2 - 1)}*\frac{(x^2-1)}{(x-1)}\end{align}$$

$$\begin{align}&\frac{tan(x^2-1}{(x-1)}=\frac{sen(x^2-1)}{(x^2-1)}*\frac{1}{\cos(x^2 - 1)}*(x+1)\end{align}$$

Y el último "truco" que usaremos es multiplicar y dividir lo anterior por el mismo valor (para que el cociente no cambie). Multiplicaremos por "x^2 - 1" quedando:
¡Y ya llegamos!... O sea:
- Cuando x tienda a uno, el primer cociente es el límite "famoso" que conocemos y que tenderá a 1.
- El segundo cociente es fácil pues cuando x tiende a 1, "x^2-1" tiende a cero, y el coseno de cero vale 1.
- Y finalmente, la última expresión tiende a 2 cuando x tiende a 1.
Resumiendo:

$$\begin{align}&\lim_{x \to 1}\frac{tan(x^2-1}{(x-1)}=\\ &\\ &=\lim_{x \to 1}\frac{sen(x^2-1)}{(x^2-1)}*\frac{1}{\cos(x^2 - 1)}*(x+1)=\\ &\\ &=1*1*2=2\end{align}$$