Calcular el área del terreno
El señor Wilfredo heredo un terreno, solo le notificaron que tiene la forma de un pétalo
r= cos 2 theta. Calcula el área del terreno.
Saludos
1 respuesta
Hagamos la gráfica.
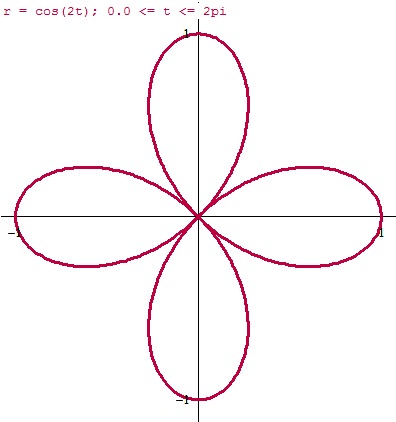
Vemos simetrías por todos los sitios. El areá es la suma de 4 pétalos iguales y casa pétalo es la suma de dos medios pétalos. Luego el área es 8 veces el área de la figura que se forma entre los ángulos 0 y pi/4
La fórmula del área para funciones dadas en forma polar es:
$$\begin{align}&A=\frac 12\int_{\alpha}^{\beta}\rho(\theta)\,d\theta\\ &\\ &\text{El área del terreno es}\\ &\\ &A=8·\frac 12\int_0^{\pi/4} \cos^22\theta\,d\theta=\\ &\\ &4\int_0^{\pi/4}\left( \frac{1+\cos 4\theta}{2}\right)d\theta=\\ &\\ &2\int_0^{\pi/4}\left( 1+\cos 4\theta\right)d\theta=\\ &\\ &\left[2\theta+\frac{sen\, 4\theta}{2}\right]_0^{\pi/4}=\frac{\pi}{2}+0-0-0=\frac{\pi}{2}\end{align}$$Y eso es todo.
Me queda una duda, la pregunta dice que el terreno tiene la forma de un pétalo y tu estas sacando el área de 4 pétalos, me explico?.
Saludos.
¿El problema no decía desde que ángulo hasta que ángulo era la función?
Creo que en mi mente quedó la palabra pétalos en vez de pétalo e hice le calculo para los cuatro. Pues si no dicen el ángulo y dicen pétalo habra que tomar la cuarta parte de lo que calcule y será
área = pi/8
Y eso es todo.
