Como se resolvería este problema si esta Por definición, la recta tangente está dada por : Y= f´(x0)(x-x0)+f(x0)
Hallar la ecuaciones de las rectas tangente y normal a la función f(x)=x^3-2x en el punto donde la recta tangente a dicha función en x=1 intersecta a la gráfica de misma función.
Respuesta de Lucas m
1
Raul Swetter!
1º calcularemos la recta tangente en x=1
2º calcularemos el punto de corte entre la recta tangente y la función
3º Buscaremos las pendientes de las rectas tangente y normal.
Recuerda que dos rectas perpendiculares m·m'=-1 (el producto de sus pendientes es -1)
4º escribiremos las ecuaciones de las rectas
Vamos alla:
$$\begin{align}&\ y=x^3-3x\\ &\\ &y '= 3x^2-3\\ &\\ &En \ x=1 \ f(1)=1-3=-2\\ &P=(1,-2)\\ & f(1)'=3-3=0\\ &P \ es \ un \ punto \ crítico\\ &recta \ tangente \ en P\\ &y=-2\\ &\\ &2º\\ &resolviendo \ el \ sistema\\ &y=-2\\ &y=x^3-3x\\ &\Rightarrow x^3-3x=-2\\ &x^3-3x+2=0\\ &Ruffini\\ &x=-2\\ &Punto \ tangencia \ T=(-2,-2)\\ &\\ &3º \\ &m=f(-2)'=9 \ pendiente \ tangente\\ &m=\frac{-1}{9} \ pendiente \ de \ la \ normal\\ &\\ &4º \\ &tangente\\ &y+2=9(x+2)\\ &y=9x+16\\ &\\ &normal\\ &y+2=\frac{-1}{9}(x+2)\\ &9y+18=-x-2\\ &-x-9y=20\\ &\\ &\end{align}$$Grafica:
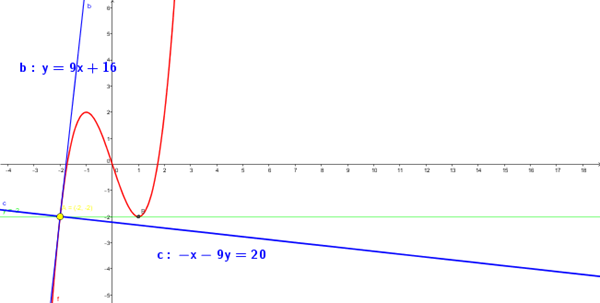
Equivocaste un dato no es 3x es 2x - Angela Parra