Como resolver el siguiente ejercicio de torema fundamental de calculo (integral definida) (7)
a) Use las siguientes formulas como guía sin tomar en cuenta la "c" ya que la integral es definida !
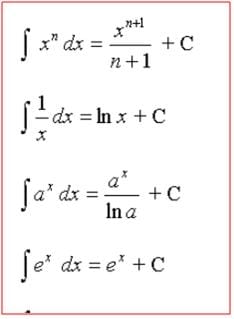
b) Resolver el siguiente ejercicio paso a paso.
7.
$$\begin{align}&\int_2^5e^{2x}dx\end{align}$$
1 Respuesta
·
Dime si ya habéis dado la resolución de integrales definidas por cambio de variable. O si al menos habéis dado la de integrales indefinidas por cambio de variable.
No es que sea imprescindible usar el cambio de variable ya que se puede resolver con algo de lógica, pero si lo habéis dado no tendré qeu dar tantas explicaciones.
saludos valeroasm
estoy perdido en lo que me preguntas la verdad no entiendo nada, disculpa por no poder aclarar.
$$\begin{align}& \end{align}$$Si no sabes lo que digo lo más probable es que no lo hayas dado, entonces vamos a hacerlo con lógica.
Tienes que calcular la integral indefinida de e^(2x)
Si derivas e^(2x) tendrás
$$\begin{align}&(e^{2x})' = 2·e^{2x}\end{align}$$Como ves obtienes lo que buscas pero multiplicado por 2. Entonces si divides entre 2 lo que vas a derivar tendrás como derivada lo que buscas
$$\begin{align}&\left(\frac{e^{2x}}{2}\right)' = e^{2x}\end{align}$$Luego ya tienes la integral indefinida, ya solo te falta evaluarla entre 2 y 5
$$\begin{align}&\int_{2}^{5}e^{2x}dx=\left.\frac{e^{2x}}{2} \right|_2^5=\frac{e^{10}-e^4}{2}\end{align}$$Y eso es todo.
