¿Pueden mostrarme el análisis del concepto de funciones continuas y discontinuas en función a su aplicación?
1.-Analizar el concepto de funciones continuas y discontinuas en función a su aplicación.

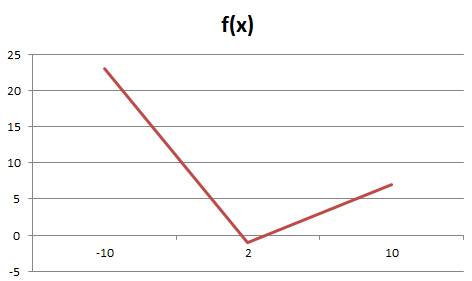
2.-La siguiente expresión representa niveles de inventario de cierta empresa, en diferentes tiempos:

Respuesta de Lucas m
1
2 respuestas más de otros expertos
Respuesta
2
Respuesta de Valero Angel Serrano Mercadal
1