Como calculo en números complejos 40,14+161, 1

$$\begin{align}& \end{align}$$

¡Hola vitor132!

·

Hay muchas igualdades ahí que no son igualdades. Cuando se escribe un signo = lo de detrás tiene que ser lo mismo que lo de delante, no se puede aprovechar para hacer sumas encadenadas ya que eso solo lo va a entender el que lo hace y si acaso el que lo esté viendo mientras se lo explican. En la literatura hay que volver a escribir el resultado otra vez en la línea siguiente si le va a sumar algo. Tampoco son de recibo esos j que aparecen milagrosamente.

Dicho eso podemos ver que

$$\begin{align}&\sqrt{86.62^2+29.69^2}=91.567...\approx91.57\\&\\&41.14\times161.1-161.1=6466.554\approx6466.55\\&\\&\sqrt{36.62^2+29.69^2}=47.14361569\approx47.14\end{align}$$

Pero lo que hay escrito no hay por donde cogerlo.

Sí es complicado sólo con lo que escribí le adjunto foto del enunciado y de los pasos que sigue igual con eso saca alguna conclusión.

Muchas gracias.

$$\begin{align}&M_{\alpha}=M(\cos\alpha+j·sen\alpha) = Mcos\alpha+j·M·sen\alpha\\&\\&47.14_{33.23º}= 47.14·\cos(33.23º)+j·47.17·sen(33.23º)=\\&\\&39.43 + j·25.85\end{align}$$

Bueno, con este desarrollo está todo mucho más claro. 

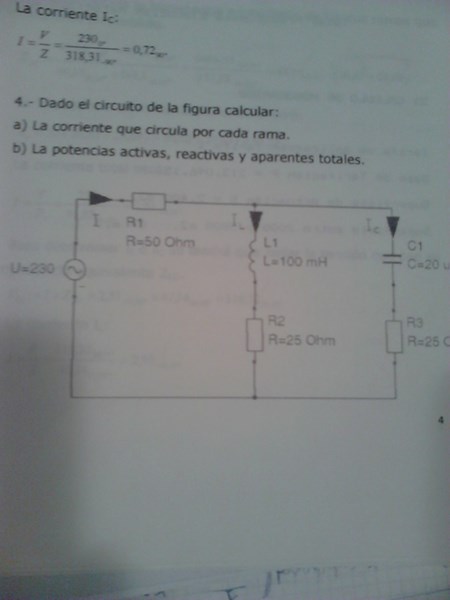
Son todo operaciones con números complejos, para las sumas emplea la forma binomial y para las multiplicaciones o divisiones la forma polar. Simplemente hay que saber cómo se opera y cómo se transforma un número complejo de una forma a otra.

El cálculo de X_L y X_C no presenta ningún problema, se aplcia la fórmula que maneja números reales y ya está.

Luego para el cáculo de las impedencias en las ramas usa unas fórmulas en que las reactancias y capacitancias se suman o restan como números imaginarios a las resistencias que son números reales.

Y una vez calculadas esas fórmulas que dan números complejos en forma binomial los transforma a forma polar.

En forma polar un número complejo tiene una parte llamada módulo y otra llamada ángulo o argumento. El módulo se obtiene como la raíz cuadrada de la suma de los cuadrados de la parte real e imaginaria. El ángulo es el arco cuya tangente mide el cociente de la parte real entre la imaginaria. Asi en la rama primera tienes:

$$\begin{align}&Z_1=25+31.41j\\&\\&Módulo = \sqrt{25^2+31.42^2}=40.14\\&\alpha=arctg\left( \frac{31.42}{25}\right)=51.48º\\&\\&\text{Y en forma polar se escribe así}\\&\\&Z_1=40.14_{51.48º}\\&\\&······\\&\text{Y en la segunda}\\&\\&Z_2=25-159.15j\\&\\&Módulo = \sqrt{25^2+159.15^2}=161.10\\&\\&\alpha = arctg\left( \frac{-159.15}{24} \right)= -81.07º\\&\\&Z_2=161.10_{-81.07º}\end{align}$$

Luego se calcula la impedancia equivalente que es el cociente entre el producto de las dos ramas y su suma.

El producto de números en forma polar tiene como módulo el producto de los módulos y como argumento la suma de los argumentos. La suma de complejos es mejor hacerla en forma binomial y lego transformarla en polar si es necesario.

Entonces el numerador es el producto de las dos impedancias

$$\begin{align}&40.14_{51.48º}\times 161.10_{-81.07º}=\\&\\&(40.14\times161.10)_{51.48º-87.07º}=\\&\\&6466.55_{-35.59}\end{align}$$

Y para el denominador hacemos la suma de la representación binomial

25 + 31.41j + 25 - 159.15j = 50 - 127.74j

y transformamos el resultado a forma polar

$$\begin{align}&Módulo=\sqrt{50^2+127.74^2}= 137.18\\&\\&\alpha=arctg\left (\frac{-127.74}{50} \right) =-68.62º\\&\\&Denominador = 137.18_{-68.82º}\\&\\&\text{Y ahora tenemos la división}\\&\\&\frac{6466.55_{-35.59º}}{137.18_{-68.82º}}=\\&\\&\text{Los módulos se dividen y el ángulo del}\\&\text{denominador se resta al del numerador}\\&\\&=\left(\frac{6466.55}{137.18}\right)_{-35.59º-(-68.82º)}=47.14_{33.23º}\end{align}$$

Y ahora convierte el número polar a binomial eso se hace así

UFFFFF!

No me sale el resultado del documento y no sé dónde puede fallar. Podrías mandar con mas resolución la linea de Z_LC, es imposible ver los subíndices.

Tal como das todo hay que adivinar !... ¿Por qué mejor no pones el enunciado real del ejercicio y lo que se pide y te lo desarrollamos paso por paso?

Bueno el ejercicio está ahora planteado y bien resuelto.

Lo que ocurre es que te estas olvidando de como se trabaja con números complejos. Concretamente te estas olvidando de los argumentos de cada Impedancia. Recorda que cada impedancia la pensas como un vector con modulo y argumento.. en el plano fasorial.

Tal como te plantean el paralelo aplican simplemente  Zeq. = Z1 Z2 / Z1 + Z2

Pero aqui Z1 = 25 + j31.41 --carga inductiva - que tambien podes escribir 40.14 con argumento = arc tg 31.41/25 = 51.48°  ...o sea lo indicas como 40.14/ 51.48° ohms

Analogamente Z2 = 25 - j 159.15- carga capacitiva - que tambien lo podes indicar como 161.1 con argumento arc tg. -159.15 / 25 = -81° ... o sea que lo indicas como 161.1 / -81° ohms

Luego la fórmula del paralelo te esta quedando :

Z eq= (40.14 / 51.48)°  x  (161.1 / -81°)  /  (40.14 / 51.48)°  +   (161.1 / -81°)

El numerador te esta dando ...(40.14 x 161.1) con argumento (51.48 - 81)

O sea 6466.55 / -29.52°

Para efectuar la suma del numerador debes poner los complejos en forma binomial.....o sea:  (25 + j31.41) + ( 25 - j 159.15) = 50 - j 127.74  lo que en forma de fasor sería....Modulo = (50^2 + 127.74^2)^1/2  =( 2500 + 16317.5)^1/3 = 137.17 y argumento arc tg -127.74/50 = -2.55°

O sea tu Zeq.del paralelo   =  (6466.55 / -29.52°)  /  (137.17 / -2.55°) =

47.14 / -26.97° ohms.

En definitiva tienes que estudiar bien números complejos... como se operan... como se transforman de binomial a fasorial y viceversa.

Suerte.