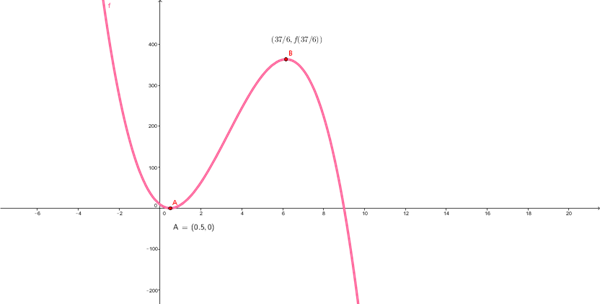
¿Como puedo determinar la siguiente función lo mas simplificada posible?
Considera la funcion
$$\begin{align}&f(x)=(2x-1)^2(9-x)\end{align}$$determina lo siguiente:
- La derivada de la función, lo más simplificada posible.
- Los valores críticos de la función.^
- Si los valores críticos son máximos o mínimos.
- Los intervalos de crecimiento y de decrecimiento de la función.
2 Respuestas
Respuesta de Lucas m
5
Respuesta de Valero Angel Serrano Mercadal
8