¿Cuál es la función de elasticidad precio de la demanda, e indique el tipo de elasticidad si el precio es de $5?
La demanda de uno de sus productos está dada por la función
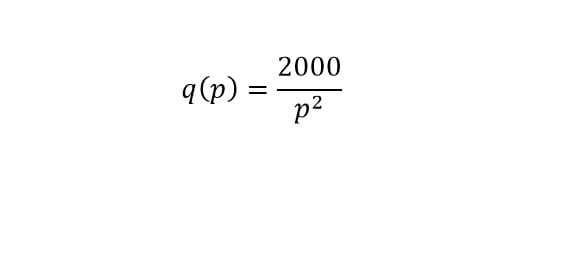
Determina la función de elasticidad precio de la demanda, e indique el tipo de elasticidad si el precio es de $5.
¿Cuál es la función de elasticidad precio de la demanda, e indique el tipo de elasticidad si el precio es de $5?
1 respuesta
·
La elasticidad de la demanda entre un punto P y otro es:
$$\begin{align}&E_p=\frac{\frac{\Delta Q}{Q}}{\frac{\Delta P}{P}}=\frac{\Delta Q}{\Delta P}·\frac PQ\end{align}$$La elasticidad en el punto P es el límite de esa expresión cuando el incremento de P tiende a 0.
Entonces el primer factor de la expresión se transforma en la derivada de Q respecto de P
$$\begin{align}&E_p(P)= \frac{dQ}{dP}·\frac{P}{Q}\\&\\&\text{Considerando Q como función del precio}\\&\\&E_p(p) = \frac{dQ(p)}{dp}·\frac{p}{Q(p)}\\&\\&\text{y con el dato que nos dan }\\&\\&Q(p)=\frac{2000}{p^2}\implies Q(5)=\frac {2000}{25}=80\\&\\&\frac{dQ(p)}{dp}=-\frac{4000}{q^3}\implies \\&\left. \frac{d Q(p)}{dp}\right|_{p=5}=-\frac{4000}{125}= -32\\&\\&E_p(5)=-32·\frac{5}{80}=-2\end{align}$$Es una demanda elástica (o relativamente elástica) ya que es menor que -1
·
Y eso es todo.
En respuesta al comentario de Tabata y como corrección de la respuesta.
Me pregunta que por qué da -4000/q^3.
No es eso sino -4000/p^3 lo que debía haber puesto, tuve una errata.
Y es eso por ser la derivada de
q(p) = 2000/p^2 = 2000·p^(-2)
q'(p) = 2000 ·(-2)p^(-3) = -4000p^(-3) = -4000/p^3
Perdón por el error.
Pide Miguel que explique con más detalle la derivación.
Tenemos que derivar
$$\begin{align}&Q(p)=\frac{2000}{p^2}\qquad \text{respecto de p}\\&\\&\text{subimos p al numedor cambiando el signo del exponente}\\&\\&Q(p)=2000·p^{-2}\\&\\&\text{Y ahora derivamos eso que es muy sencillo}\\&\text{recordando estas dos reglas}\\&\\&(k·f(x))' = k·f'(x)\\&\\&(x^n)'=n·x^{n-1}\\&\\&\text {entonces}\\&\\&Q'(p) =(2000·p^{-2})' = 2000·(p^{-2})'= \\&\\&2000·(-2)p^{(-2-1)}= -4000·p^{-3}\end{align}$$Y eso es todo.
Porque da -4000/q^3. Tengo esa duda. Saludos - Tabata Real
Hola profesor, se que ya se lo preguntaron pero podría explicar más detalladamente la derivación que preguntó Tabata, la verdad no le entiendo, gracias! - Miguel Vazquez
Ya hice la derivada con todo detalle Miguel - Valero Angel Serrano Mercadal