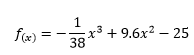¿Cuál es la derivada de la función f(x)= -1/38x^3+9.6x^2-25?

Te anexo el resultado de la derivada:

$$\begin{align}&f(x) = \frac{-1}{38}x^3 + 9.6x^2-25\\& \\&f(x) = \frac{-3}{38}x^2 + 19.2x\end{align}$$

Eso es lo más simplificado.

·

1)

La derivada es:

$$\begin{align}&f'(x)=-\frac 3{38}x^2+19.2x\\&\\&\text{o si les parece más simplicado esto, adelante}\\&\\&f'(x) = \left(\frac 3{38}x+19.2  \right)x\end{align}$$

2)

Los valores criticos de la función son los que anulan la derivada primera. Para ellos tomaremos mejor la segunda expresión y los valores críticos son los que anulan a alguno de los factores.

Para anular al factor x debe ser x=0 ese es un punto crítico.

Y el otro sale de hacer

-(3/38)x + 19.2 = 0

(3/38)x = 19.2

x = 19.2 · 38 / 3 = 243.2

Luego los puntos críticos son x=0  y  x=243.2

·

3) 

Hallamos la derivada segunda para calcular si son máximos o mínimos porque nos lo dicen, pero a veces se puede deducir sin calcularla.

f ''(x) = -(6/38)x + 19.2 = - (3/19)x + 19.2

y calculamos el valor de la derivada segunda en los puntos críticos

f ''(0) = -(3/19)·0 + 19.2 = 19.2

como es un valor positivo, x=0 es un mínimo relativo

f ''(243.2) = -(3/19)(243.2) + 19.2 = -19.2

Como es un valor negativo tenemos que x=243.2 es un máximo relativo

·

4)

Los intervalos de crecimiento o decrecimiento están delimitados por las raíces de la derivada primera. El cálculo del signo se hace sabiendo como es la gráfica de un polinomio de grado 2 con coeficiente de x^2 negativo o tomando un punto interior de cada intervalo y calculando el valor de la derivada primera en él.

Esta segunda forma te la dejo a ti como ejercicio si no te convence la primera.

Entonces la forma de calcular el signo de la derivada primera es esta:

f'(x) = -(3/38)x^2 + 19.2x

Es una parábola con el vértice hacia arriba. Empieza por la izquierda valiendo -infinito, cruza a positivo cuando llega a la raíz x=0, sigue siendo positivo hasta llegar a la otra raíz x=243.2 y termina en negativo hasta llegar a - infinito.

Luego los intervalos son

(-oo, 0)         f'(x)<0 ==> f decreciente

(0,  243.2)    f'(x)>0 ==> f creciente

(243.2,  oo)  f'(x)<0 ==> f decreciente

·

Los intervalos de concavidad y convexidad los delimitan las raíces de la derivada segunda

f ''(x) = - (3/19)x + 19.2

- (3/19)x + 19.2 = 0

(3/19)x = 19.2

x=19.2 · 19/3 = 121.6

Ese es el punto de inflexión x=121.6

Y el signo de la derivada segunda viene dado porque es una recta con pendiente negativa, que empieza valiendo infinito y llega a -infinito, luego antes de la raíz es positivo y después negativo

(-oo, 121.6)  f ''>0  ==> f es cóncava hacia arriba,  forma de U

(121.6, oo)   f''<0  ==> f es cóncava hacia abajo,  foma de iglú.

·

5) El punto de inflesión ya se había calculado antes x=121.6, si quieres calcular la coordenada y del punto calculas f(121.6) te lo dejo como ejercicio.

·

Y eso es todo.