Como calcular la probabilidad para este ejercicio sobre variables aleatorias.
Hola Mr. Valero, solicito su ayuda en la solución de este ejercicio de probabilidad, no se como plantear el ejercicio, que a continuación le planteo. Esperando que me pueda ayudar gracias
En una fábrica una de las máquinas que elabora tornillos milimétricos se averió, razón por la cual gran cantidad de tornillos al elaborarse resultaron defectuosos. Con la finalidad de evitar pérdidas, en cada caja de 40 tornillos se colocan cinco defectuosos (35 sin defectos). El vendedor de tornillos comienza a recibir reclamos por los defectuosos y decide cambiar de proveedor si antes del cuarto de los siguientes envíos recibe una caja donde al revisar aleatoriamente ocho tornillos se encuentran tres o más defectuosos. De acuerdo al contexto anterior contesta: ¿cuál es la probabilidad de que el vendedor cambie de proveedor? Justifica muy bien tu respuesta.
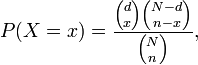


Calcule 1.5% de que cambie de empresa - lautaro capo
¿Es una afirmación? No, la probabilidad de cambio de empresa es el 4.57%. Si no espón tus cuentas o di en qué me equivoqué. Saludos. - Valero Angel Serrano Mercadal