Resolver los problemas de programación maximizar
Dados los siguientes problemas de programación:
Maximizar:
Z = 3x1+x2
Sujeto a:
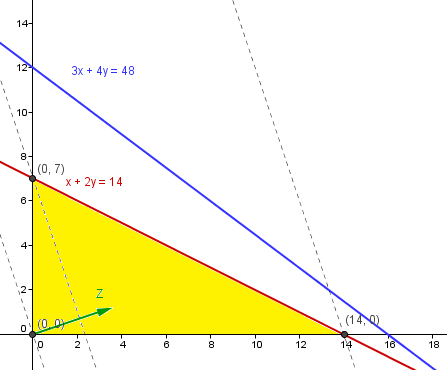
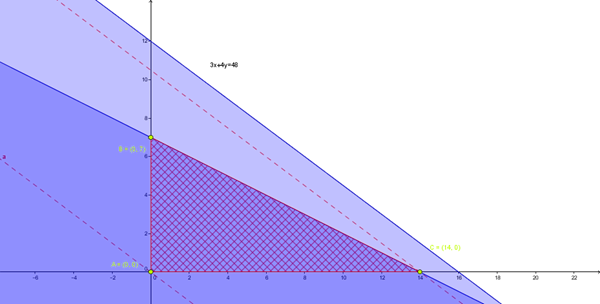
3x1+4x2<= 48
3x1+6x2<= 42
x1, x2 >= 0
Resolverlos gráficamente
2 Respuestas
·
Dibujadas las rectas de las restricciones y calculado el lado correspondiente a la inecuación resulta que la región factible es la coloreada de color amarillo y el máximo estará en un de sus cuatro vértices. En verde tienes la función objetivo, los puntos de igual valor son líneas perpendiculares a ella y tienen mayor valor cuanto más alejadas están de (0,0).
La más alejada que pase por los vértices es la que pasa por (14,0)
El máximo se conseguirá con
x1=14
x2=0
·
Y eso es todo.
Graficando:
La Región Factible es la cuadriculada, está por debajo de las dos rectas
z(A)=0
z(B)=3·0+7=7
z(C)=3·14+0=42 Máximo en C=(14,0)