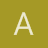Ejercicio de vectores con ángulos
En un poste telefónico se enrolla una cuerda, como se muestra en la figura, formando un ángulo de 120º. Si se tira de un extremo con una fuerza de 60 Newtons, y del otro con una fuerza de 20 Newtons, ¿cuál es la fuerza resultante sobre el poste telefónico y qué ángulo forma con la semirrecta horizontal positiva?
2 Respuestas
Por un lado el enunciado no esta muy claro... Suponemos que estas viendo desde arriba al poste y que las fuerzas son aplicadas tirando desde abajo. Obviamente ambas fuerzas te definen un plano.
La resultante podrías calcularla por el teorema del coseno :
R = (60^2 + 20^2 - 2 x 60 x 20 x cos 60°)^1/2 = 53 N
"Semirrecta horizontal positiva" ... entenderíamos que seria el que forma con la fuerza de 60 N ... sería aplicando el teorema del seno:
R/ sen 60° = 20/ sen fi ........................sen fi = 20 N sen 60° / 53 N = 0.3268 .......fi= 19°
Ya se ve la imagen, debió ser un fallo momentáneo del servidor de la imagen.
No se ve el poste, pero haremosla suma de vectores que aparece en la imagen
$$\begin{align}&\text{El vector horizontal es}\\&\\&u = (60, 0)\\&\\&\text{y el otro es}\\&\\&v = (20cos 120º, 20sen 120º) =\\&\\&\left(-20·\frac 12, \;20·\frac {\sqrt 3}{2} \right)= (-10,\;10 \sqrt 3)\\&\\&\text{La fuerza resultante es}\\&\\&u+v=(60-10,\;10 \sqrt 3)=\\&\\&(50N,\;10 \sqrt 3N) \approx (50N,\;17.32N)\\&\\&\text{su módulo es}\\&\\&\sqrt{50^2+17.32^2}= 52.91486N\\&\\&\text{Y el ángulo es}\\&\\&\alpha=tg^{-1}\left(\frac{17.32}{50}\right)=19.1061º\end{align}$$Y eso es todo.
¡Gracias! La verdad me resulta difícil encontrar respuestas que me ayuden a entender el tema, suelo analizar el cómo de las respuestas, y he visto su trabajo con operaciones de cálculo, espero aprender "bien" y algún día ayudar como lo hace usted.