Ejemplo de función cuyo conjunto de puntos donde es continua es denso y no es integrable
Me preguntan:
Diga si es verdadera o falsa la siguiente afirmación. En caso de ser verdadera, demostrarla; en caso de ser falsa, dar un ejemplo que lo muestre demostrando que cumple la tesis y que no cumple la consecuencia. La afirmación es:
"Si el conjunto de puntos donde f es continua, es denso en un rectángulo R, entonces f es integrable sobre R" (f es una función con dominio en el plano y toma valores en los reales).
Se que hay un teorema que garantiza que si tenemos una función f integrable en un rectángulo R contenido en el plano, entonces el conjunto de puntos donde f es continua es denso en el rectángulo R.
Luego, me están preguntando si el recíproco se cumple o no.
Intenté demostrarlo, como si fuera verdad. Supuse que f no era integrable en R y traté de llegar a una contradicción; pero en ese camino necesitaba poder garantizar que el conjunto de discontinuidades de f fuera Lebesgue medible y ésto no lo puedo garantizar de ninguna manera.
Entonces supongo que la afirmación es falsa, pero no logro construir una función tal que el conjunto de puntos donde sea continua sea denso en el rectángulo R, y que no sea integrable en R.
Agradeceré mucho cualquier idea que pueda servir para resolver esto.
1 Respuesta
Ya logré resolverlo.
Hay que construir un conjunto de Cantor "extendido", que denotamos con la letra C, que tenga medida (de lebesgue) mayor que 0.
Lo construimos de la siguiente manera.
Paso 1. Eliminamos del intervalo [0, 1] un intervalo centrado en el intervalo, de longitud 1/(2*3) el intervalo E01 = (5/12, 7/12)
Y sea C1 = [0, 5/12] U [7/12, 1].
Paso 2. Eliminamos de cada intervalo de C1, un intervalo centrado, de longitud 1/(2*3^2) = 1/18. A esos dos intervalos abiertos les llamamos E11 y E12.
Y hacemos C2 = unión de los 4 intervalos cerrados que quedan.
Y así sucesivamente, en el paso k, habremos construido Ck con la unión de 2^k intervalos cerrados; y Ck+1, lo construimos eliminando de Ck 2^k intervalos abiertos, cada uno de longitud 1/[2*3^(k+1)].
Definimos el conjunto C de Cantor, como la intersección infinita y numerable de todos los Ck.
En cada paso k, la medida de los intervalos abiertos que quitamos, es:
2^k * (1 / [[2*3^(k+1)])
Luego, sumamos la medida de todos los abiertos que vamos quitando hasta el paso n, y nos queda:
1 /(2 · 3) + 2 / [ 2 ( 3^ 2)] + 2^2 / [2 · (3^3)+ · · · + 2n / [ 2 · (3^n+1)]
= 1/2 [1 − (2/3)^( n+1)] .
Luego, si n tiende a infinito, tendremos que la unión infinita de todos los abiertos que fuimos quitando al intervalo [0, 1], es igual a 1/2. Por tanto el Cantor C, también tiene medida 1/2.
Así C es compacto, infinito no numerable, cerrado, sin puntos interiores y sin puntos aislados.
Ahora definimos f(x) = 0 si x no está en C, y f(x) = 1 si x está en el C.
El conjunto K = [0,1] - C, es denso en [0,1], pues si no fuera denso significaría que existe un intervalo contenido en C, lo que no es posible, pues C no tiene puntos interiores.
K está formado por unión de intervalos abiertos, donde f es continua (es la constante 1 en cada uno de esos intervalos).
Y f es discontinua en C, pues en cada intervalo con centro en un c en C, por pequeño que sea el intervalo, hay puntos de K. Como C tiene medida 1/2, f no es integrable en [0,1]
Ya logré resolverlo.
Hay que construir un conjunto de Cantor "extendido", que denotamos con la letra C, que tenga medida (de lebesgue) mayor que 0.
Lo construimos de la siguiente manera.
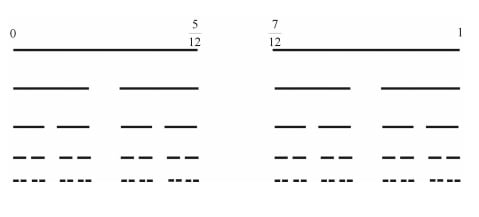
Paso 1. Eliminamos del intervalo [0, 1] un intervalo centrado en el intervalo, de longitud 1/(2*3) el intervalo E01 = (5/12, 7/12)
Y sea C1 = [0, 5/12] U [7/12, 1].
Paso 2. Eliminamos de cada intervalo de C1, un intervalo centrado, de longitud 1/(2*3^2) = 1/18. A esos dos intervalos abiertos les llamamos E11 y E12.
Y hacemos C2 = unión de los 4 intervalos cerrados que quedan.
Y así sucesivamente, en el paso k, habremos construido Ck con la unión de 2^k intervalos cerrados; y Ck+1, lo construimos eliminando de Ck 2^k intervalos abiertos, cada uno de longitud 1/[2*3^(k+1)].
Definimos el conjunto C de Cantor, como la intersección infinita y numerable de todos los Ck.
En cada paso k, la medida de los intervalos abiertos que quitamos, es:
2^k * (1 / [[2*3^(k+1)])
Luego, sumamos la medida de todos los abiertos que vamos quitando hasta el paso n, nos queda:
1 /(2 · 3) + 2 / [ 2 ( 3^ 2)] + 2^2 / [2 · (3^3)+ · · · + 2n / [ 2 · (3^n+1)]
= 1/2 [1 − (2/3)^( n+1)] .
Si n tiende a infinito, tendremos que la unión infinita de todos los abiertos que fuimos quitando al intervalo [0, 1], es igual a 1/2. Por tanto el Cantor C, también tiene medida 1/2.
Así C es compacto, infinito no numerable, cerrado, sin puntos interiores y sin puntos aislados.
Ahora definimos f(x) = 0 si x no está en C, y f(x) = 1 si x está en el C.
El conjunto K = [0,1] - C, es denso en [0,1], pues si no fuera denso significaría que existe un intervalo contenido en C, lo que no es posible, pues C no tiene puntos interiores.
K está formado por unión de intervalos abiertos, donde f es continua (es la constante 1 en cada uno de esos intervalos).
Y f es discontinua en C, pues en cada intervalo con centro en un c en C, por pequeño que sea el intervalo, hay puntos de K. Como C tiene medida 1/2, f no es integrable en [0,1]
