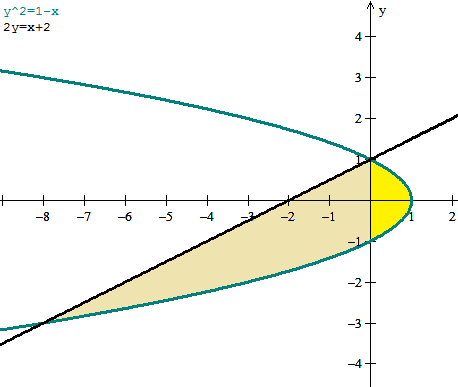
Hallar el área acotada por las gráficas y^2=1-x, 2y=x+2
La pregunta es del tema "área entre curvas" y deseo saber cómo hallar el área acotada por las gráficas y^2=1-x y 2y=x+2
2 respuestas
Respuesta de Valero Angel Serrano Mercadal
4
Respuesta
3