¿Cómo se resuelven estas integrales indefinidas?
Tengo que hallar las integrales siguientes:
A) (1/x) ((x+1)/x))^(1/2)
B) (x^(1/2))/(x^(1/2)-3)
1 Respuesta
$$\begin{align}& \end{align}$$¡Hola Pedro!
·
$$\begin{align}&\int \frac 1x \sqrt{\frac{x+1}{x}}dx=\\&\\&t^2=\frac{x+1}{x}=1+\frac 1x \implies x=\frac{1}{t^2-1}\\&\\&2t\,dt= -\frac{dx}{x^2}\implies \frac{dx}x=-2tx\,dt\implies\\&\\&\frac {dx}x=-\frac{2t}{t^2-1}dt\\&\\&=-\int t·\frac{2t}{t^2-1}dt=\\&\\&-\int \left(2 +\frac{2}{t^2-1} \right)dt=\\&\\&\text{se hacen fracciones simples a ojo}\\&\text{o las haces con el método fácilmente}\\&\\&-2t-\int\left(\frac{1}{t-1}-\frac{1}{t+1} \right)dt=\\&\\&-2t-log|t-1|+log|t+1|+C=\\&\\&log \left|\sqrt{\frac{x+1}{x}}+1\right| -log \left|\sqrt{\frac{x+1}{x}}-1\right|-2 \sqrt{\frac{x+1}{x}}+C\\&\\&\\&\end{align}$$No ha sido fácil, manda la otra integral en otra pregunta
No entendí el método de porqué cambiar a t^2 y el resultado no coincide con el de wolfram. Espero pueda aclarar mis dudas. Saludos.
El cambio es el cambio que tu quieras. Con tal pongas un
f(x) = g(t) ya queda detrermionada el cambio, luego te las apañas para relacionar de modo adecuado la x y la t y la dx y la dt y hacer el cambio
Es mejor hacer el cambio
t^2 = (x+1)/x
que el cambio
t = sqrt[(x+1)/x]
Y antes de mirar Wolfram Alpha supongo que habrán usado las propiedades de los logaritmos, luego te aventurao una respuesta más simplificada y luego miro la página esa que es buena, pero alguna vez te da sorpresas y usa algunos métodos muy raros.
$$\begin{align}&log \left|\sqrt{\frac{x+1}{x}}+1\right| -log \left|\sqrt{\frac{x+1}{x}}-1\right|-2 \sqrt{\frac{x+1}{x}}+C=\\&\\&log \frac{\left|\sqrt{\frac{x+1}{x}}+1\right|}{\left|\sqrt{\frac{x+1}{x}}-1\right|}-2 \sqrt{\frac{x+1}{x}}+C=\\&\\&log \left|\frac{\sqrt{x+1}+\sqrt x}{\sqrt{x+1}-\sqrt x} \right|-2 \sqrt{\frac{x+1}{x}}+C=\\&\\&log|(\sqrt{x+1}+\sqrt x)^2|-2 \sqrt{\frac{x+1}{x}}+C=\\&\\&2\,log(\sqrt{x+1}+\sqrt x)-2\sqrt{\frac{x+1}{x}}+C\end{align}$$Bueno esa pienso yo que es la respuesta más simplificada que se puede dar. Voy a ver que dice Wolfram Alpha
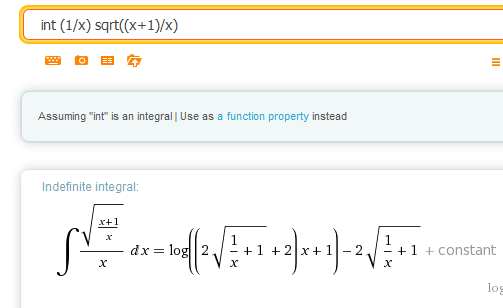
Pues no veo nada edificante la respuesta de Wolfran Alpha, se han dejado un factor 2 dentro que siendo logaritmos será un +log2 que es una constante que sobra.
Antes de nada decirte que en la integrales cuya respuesta es logaritmos o funciones trigonométricas se pueden expresar de mil maneras, lo que pasa es que aunque no lo parezca serán expresiones iguales salvo una constante.
$$\begin{align}&log\left(\left(2 \sqrt{\frac{1}{x}+1}+2 \right)x +1 \right)-2 \sqrt{\frac 1x+1}+C=\\&\\&log2\,+log \left(\left( \sqrt{\frac{1+x}{x}}+1 \right)x +1 \right)-2 \sqrt{\frac {1+x}x}+C=\\&\\&\text{El log 2 es una constante, va al contenedor de las constantes}\\&\\&log \left(\left(\frac{\sqrt{x+1}+\sqrt x}{\sqrt x} \right)x +1 \right)-2 \sqrt{\frac {1+x}x}+C=\\&\\&log \left(\left(\sqrt{x+1}+\sqrt x \right)\sqrt x +1 \right)-2 \sqrt{\frac {1+x}x}+C\end{align}$$Bueno, es difícil demostrar que sea la misma, lo que voy a hacer es demostrarte que la mía esta bien.
$$\begin{align}&f(x)=2\,log(\sqrt{x+1}+\sqrt x)-2\sqrt{\frac{x+1}{x}}+C\\&\\&f'(x)=2 ·\frac{\frac{1}{2 \sqrt{1+x}}+\frac{1}{2 \sqrt x}}{\sqrt{x+1}+\sqrt x}-2 ·\frac{\frac{x-(1+x)}{x^2}}{2 \sqrt{\frac{1+x}{x}}}=\\&\\&\frac{\frac{1}{\sqrt{1+x}}+\frac{1}{\sqrt x}}{\sqrt{x+1}+\sqrt x}+\frac{\frac{1}{x^2}}{\sqrt{\frac{1+x}{x}}}=\\&\\&\frac{\frac{\sqrt x+ \sqrt{x+1}}{\sqrt{x+1}\sqrt x}}{\sqrt{x+1}+\sqrt x}+\frac{\sqrt x}{x^2 \sqrt{1+x}}=\\&\\&\frac{1}{\sqrt{x+1}\sqrt x}+\frac{1}{x \sqrt x \sqrt{x+1}}=\\&\\&\frac{1}{\sqrt x \sqrt{1+x}}\left(1+\frac 1x \right)=\\&\\&\frac{1}{\sqrt x \sqrt{1+x}}\left(\frac{1+x}{x} \right)=\\&\\&\frac{\sqrt{1+x}}{\sqrt x ·x}=\frac 1x \sqrt{\frac{1+x}{x}}\end{align}$$Y queda demostrado que la mía está bien. Y más no se me puede pedir, yo soy responsable de lo que haga yo, no de lo que haga Wolfram Alpha.
