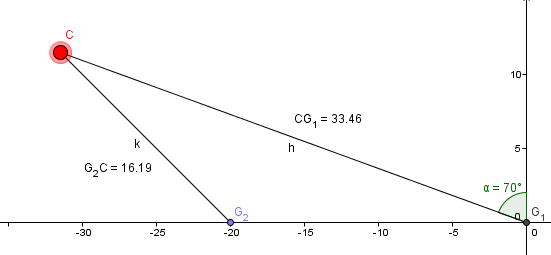
Determine la distancia del incendio a cada uno de los guardabosques.
Un guardabosque observa con un rumbo de N70°O algo que parece incendio. Se comunica con otro guardabosque ubicado a 20 Km al oeste de él, quien le confirma que se trata de un incendio y que su rumbo con respecto al incendio es de N45°O. Determine la distancia del incendio a cada uno de los guardabosques.
2 Respuestas
Hola,
No poseo dibujo del ejercicio, N70ºO tiene que ver con los puntos cardinales Rumbo norte 70 grados al oeste, algo así, para el calculo solamente se toman los grados.
Yo sigo sin entender si los 70º se forman con la horizontal o la vertical. Pero si fuesen con la horizontal las líneas de los dos observadores no se cortarían al norte sino al sur, luego deben ser con la vertical. Entonces los auténticos ángulos referidos al sistema de coordenadas habitual, donde el este es la dirección positiva del eje X, son 160º y 135º
La posición del incendio para el primer guadabosque será:
(h·Cos 160º, h·sen 160º)
Donde h es la distancia del guardabosque primero al incendio.
La posición según el segundo guardabosque es
(-20+k·cos 135º, k·sen 135º)
Siendo k su distancia al incendio. Como la posición es la misma tenemos estas dos ecuaciones en h y k
h·cos 160º = -20+k·cos 135º
h·sen 160º = k·sen 135
Pero no me gustan esos números, si reflejamos la figura en el eje Y se mantienen las distancias y queda
h·cos 20º = 20 + k·cos 45º
h·sen 20º = k·sen45º
Si dividimos la segunda entre la primera queda
$$\begin{align}&\frac{sen\,20º}{\cos 20º} = \frac{k·sen\,45º}{20+k·\cos 45º}\\&\\&tg\,20º=\frac{k·sen\,45º}{20+k·\cos 45º}\\&\\&tg\,20º·(20+k·\cos 45º)=k·sen\, 45º\\&\\&k·tg\,20º· \cos 45º - k·sen\,45º = -20·tg\,20º\\&\\&k=-\frac{20·tg\,20º}{tg\,20º· \cos 45º - sen\,45º}=16.185772km\\&\\&\\&\text{Y la ecuación segunda era }\\&h·sen\,20º=k·sen\, 45º\\&\text{luego}\\&\\&h= k·\frac{sen\,45º}{sen\,20º}= 33.46314km\end{align}$$Luego el primer guardabosque está a
33.46314km
Y el segundo a
16.185772km
Como veo que hay polémica aquí está el gráfico.
Y eso es todo.
D1 Distancia al fuego del guardabosques 1
D2 Distancia al fuego del guardabosques 2
* (incendio)
|\ \
h | \ d1 \ d2
| \ \
| \ \
<----->70º \
<------------------ > 45º
<--------->
20 km
* (incendio)
|\ \
h | \ d1 \ d2
| \ \
| \ \
----->70º >45º
<-----><------>
x x+20
tg 70=h/x
tg 45=h/(x+20)
h=tg70*x
h=tg45(x+20) --->tg 45=1
h=x+20
Se igualan las alturas
tg70*x=x+20
(tg 70-1)*x =20
x=20/(tg 70-1)
x=11.445 km
cos 70=11.445/d1
d1=11.445/cos(70)= 33.463 km
cos 45=(11.445+20)/d2
d2=31.445/cos 45 = 44.47 km