Como definir una función a partir de la cónica dada?

·

La cónica es y² - 3x + 2 = 0

No se si quieres ponerla como función o calcular sus elementos

Las parábolas tienen dos formas canónicas

(y-k)² = 2p(x-h)

(x-h)² = 2p(y-h)

Donde (h, k) es el vértice y p es la distancia entre el foco y la directriz. El vértice está siempre a mitad de camino del foco y directriz luego a p/2 del foco y p/2 de la directriz.

Si p es positivo el orden en la dirección positiva del eje de la parábola es directriz, vértice, foco; son formas de U o de C.

Si p es negativo se invierte el orden: directriz, vértice, foco.

Esta de aquí se ve que es de la primera forma y es fácil de ponerla en forma canónica

y² =3x-2

$$\begin{align}&y^2 = 2·\frac 32\bigg(x - \frac 23\bigg)\end{align}$$

Luego es una parábola con vértice en (2/3, 0)

La distancia entre directriz y foco es 3/2 y es positiva, luego va primero la directriz, después el vértice y finalmente el foco. El eje es el de la variable que no está al cuadrado, luego el eje X. Recuerda que la parábola normal es y=ax²+bx+c, y tiene el ejeY de ahí he extraído la regla para calcular el eje.

Luego a distancia -p/2 del vértice en el eje X estará la directriz

$$\begin{align}&\frac 23-\frac 34=\frac{8-9}{12}=-\frac 1{12}\\&\\&\text{la ecuación de la directriz es}\\&\\&x=-\frac 1{12}\\&\\&\text{Y el foco a distancia p/2 del vértice}\\&\text{en la dirección del eje X}\\&\\&\bigg(\frac 23,0\bigg)+\bigg(\frac{3}{4},0\bigg)=\\&\\&\bigg(\frac 23+\frac 34,0\bigg)=\bigg(\frac{17}{12},0  \bigg)\end{align}$$

Esta es la gráfica:

Y es es todo.

¡Gracias! Profesor en la guía dice ponerla como función

Me equivoqué en la segunda forma canónica, puse

(x-h)² = 2p(y-h)

y es

(x-h)² = 2p(y-k)

Donde (h, k) es el vértice.

·

Lo que he hecho es el típico ejercicio de hallar los elementos y graficar la cónica.

Si lo único que te pedían era pasarlo a función puedes optar por hacerla una función x=f(y) que es la única que te dará toda la cónica

$$\begin{align}&y^2 - 3x + 2 = 0\\&\\&3x=y^2+2\\&\\&x=\frac{y^2+2}{3}\end{align}$$

Por que si quieres ponerlo como función y=f(x) se necesitan dos funciones para dar toda la cónica

$$\begin{align}&y^2 - 3x + 2 = 0\\&\\&y^2= 3x-2\\&\\&y= f_1(x)= \sqrt{3x-2}\\&\\&y=f_2(x)=-\sqrt{3x-2}\end{align}$$

Y eso es lo que puedo decirte, este no es un ejercicio típico y depende de cómo te hayan enseñado que hay que hacerlo.

Hay profesor no entendí, cuando le dije que me la pedían como función, ¿sera qué usted me la manda nuevamente pero como función?

Ya te dije que este ejercicio no es normal. Que depende de las ocurrencias de quien lo haya diseñado. La única forma de saber lo que quiere es si saliese en la teoría o se hubiese hecho un ejercicio parecido o igual.

Si a mi me dices, a partir de la cónica y²-3x+2=0 define una función, la única respuesta válida para mí es

$$\begin{align}&y^2-3x+2=0\\&\\&3x=y^2+2\\&\\&x=\frac{y^2+2}{3}\\&\\&\text{Luego la función será una función de y, y será esta}\\&\\&f(y)=\frac{y^2+2}{3}\end{align}$$

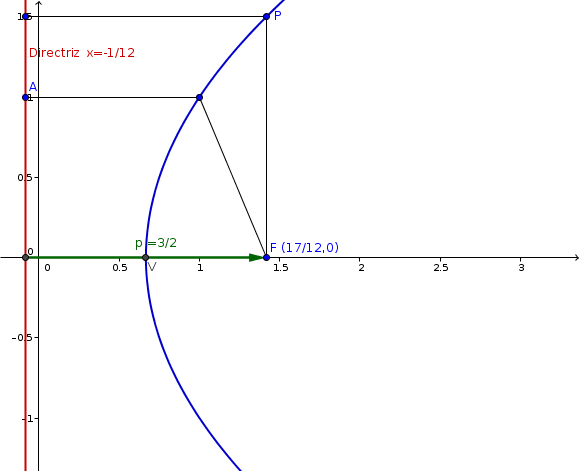
Y eso es todo.