Variables aleatorias y distribuciones de probabilidad

La función de probabilidad deseada es la hipergeométrica.

$$\begin{align}&f(x) = \frac{{Np \choose x}{Nq \choose n-x}}{{N \choose n}}\\&E(x) = np\\&V(x) = npq \frac{N-n}{N-1}\\&Donde:\\&Np+Nq = N\\&p+q=1\\&y\ en\ este\ problema\\&N = 8\\&Np=2\\&Nq=6\\&p=\frac{2}{8}=0.25\\&q=\frac{6}{8}=0.75\\&n=3\\&Quedando...\\&f(x) = \frac{{2 \choose x}{6 \choose 3-x}}{{8 \choose 3}}\\&E(x) = 3*0.25=0.75\\&V(x) = 3*0.25*0.75 \frac{8-3}{8-1}=0,4017857...\\&\end{align}$$

El diagrama de árbol es:

D: Es el suceso defectuoso

NoD: es el suceso no defectuoso

Calculemos las probabilidades de todas las ramas:

$$\begin{align}&P(D,D,noD)=\frac{2}{8}·\frac{1}{7}·\frac{6}{6}=\frac{12}{336}\\&\\&P(D,noD,D)=\frac{2}{8}·\frac{6}{7}·\frac{1}{6}=\frac{12}{336}\\&\\&P(D,noD,noD)=\frac{2}{8}·\frac{6}{7}·\frac{5}{6}=\frac{60}{336}\\&\\&P(noD,D,D)=\frac{6}{8}·\frac{2}{7}·\frac{1}{6}=\frac{12}{336}\\&\\&P(noD,D,noD)=\frac{6}{8}·\frac{2}{7}·\frac{5}{6}=\frac{60}{336}\\&\\&P(noD,noD,D)=\frac{6}{8}·\frac{5}{7}·\frac{2}{6}=\frac{60}{336}\\&\\&P(noD,noD,noD)=\frac{6}{8}·\frac{5}{7}·\frac{4}{6}=\frac{120}{336}\\&\\&Sea  \ x=nº \ defectuosas\\&\\&P(x=0)=\frac{120}{336}\\&\\&P(x=1)=\frac{60}{336}·3=\frac{180}{336}\\&\\&P(x=2)=\frac{12}{336}·3=\frac{36}{336}\\&\\&P(0)+P(1)+P(2)=1\\&\\&E(x)= \sum x_i·P_i=0·\frac{120}{336}+1·\frac{180}{336}+2·\frac{36}{336}=\frac{252}{336}=\frac{3}{4}=0.75\\&\\&V(x)= \sum x_i^2·P_i-E^2=0·\frac{120}{336}+1^2·\frac{180}{336}+2^2·\frac{36}{336}-(\frac{3}{4})^2=\frac{45}{112}=\\&0.4017857143\\&\\&S(x)=\sqrt{V(x)}=\sqrt{\frac{45}{112}}=\frac{3 \sqrt{35}}{28}=0.633865691\\&\\&\end{align}$$

·

La distribución es una hipergeométrica tal como hizo Gustavo. Pero el problema muchas veces es que te olvides de la complicada expresión de la probabilidad de esa distribución. Entonces puedes hacelo por deducción.

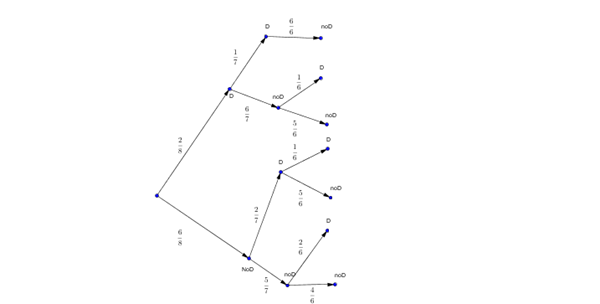
Un embarque de 8 televisores contiene 2 unidades defectuosas. Un hotel realiza una compra al azar de 3 de los televisores.

Si X es una variable aleatoria discreta que representa el número de unidades defectuosas que compra el hotel:

a.- Encuentre la función de probabilidad f(x)

b.- Encuentre el valor esperado E(x), la varianza V(x) y la desviación estándar S(x)

Tomas las combinaciones posibles de la compra, esos son los casos posibles

C(8,3) = (8·7·6) / 3! = 56

Y ahora los casos favorables para x (que en realidad son malos porque significa número de televisores malos.

Habrá un caso de estos cuando haya x entre los 2 malos y haya 3-x entre los buenos que son 8-2=6

Luego los casos favorables son

C(2,x)·C(6,3-x)

Luego la probabilidad(casos favorables/ casos posibles es)

P(x) = C(2,x)·C(6,3-x) / 56

Que si quieres podemos poner en bonito

$$\begin{align}&P(x) = \frac{\binom 2x\binom{6}{3-x}}{56}\end{align}$$

·

b)

Y la esperanza y varianza es algo bastante complejo de deducir, luego aquí no quedará mas remedio que echar mano de la teoría sobre la distribución hipergeométrica que dice

E(X) = nd/N

donde

N=población

n=muestra

d=elementos que cumplen la condición

E(X) = 3·2/8 = 6/8 = 3/4 = 0.75

·

$$\begin{align}&Var[X]=\frac{8-3}{8-1}·\frac{3·2}{8}·\left(1-\frac 28  \right)=\\&\\&\frac 57·\frac 34·\frac 34=\frac {45}{112}= 0.4017857143\end{align}$$

Si acaso, si quisieras pon otra pregunta y calculo manualmente la esperanza y varianza que en este ejemplo tan sencillo no costaría mucho hacerlo.