Ejercicio de física mecánica las tensiones en las dos partes de la cuerda. B) Encuentre el momento de inercia de la polea.
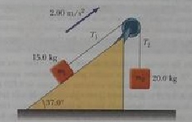
Dos bloques, como se muestra en la figura P10.71, están conectados mediante una cuerda de masa despreciable que pasa sobre una polea de 0.250 m de radio y momento de inercia I. El bloque sobre el plano inclinado sin fricción se mueve hacia arriba con una aceleración constante de 2.00 m/s2. A) Determine T1 y T2, las tensiones en las dos partes de la cuerda. B) Encuentre el momento de inercia de la polea.
2 Respuestas
Aquí debes plantear las ecuaciones correspondientes en base a :
Analizas todo sobre los diagramas de cuerpo libre sobre cada masa de tu figura así como sobre la polea.
Masa 1 = m1 = masa de la izquierda. ( subiendo)
Masa 2 = m2 = masa de la derecha ( bajando)
La aceleración la supones igual en todo el tramo ya que la cuerda no se estira ni se acorta... o sea a1 = a2 = a(tangencial) de la polea= 2 m/seg2
Tension 1 = T1 …………………………Tensión 2 = T2
Aquí las tensiones de cada lado de la cuerda son distintas porque la polea absorbe un momento torsor para acelerarse.
Sobre m1 …………………… T1 – m1g sen 37° = m1 a = 2 m1
Sobre m2 ……………………m2g – T2 = m2 a = 2 m2
Sobre la polea …………….Momento torsional = I o . a (tangencial) / (Radio)
Luego T1 = 2m1 + m1 g sen 37° = 30 N + 90.27 n = 120.3 N
T2 = m2 g - 2m2 = 200 N – 40 N = 160 N
Momento torsional sobre polea = -T1. r + T2.r = -30 + 40 = 10 Nm.
Luego Io =momento de Inercia de la polea = 10 Nm x r / aceleración = 1.25 Kg.m2