Problema de fuerza eléctrica con tres partículas (física)

·

Pudiera parecer que hay tres incógnitas pero qo no es necesario calcularla, lo que hay que hacer es calcular la relación entre q y Q que hace que en ese punto el campo sea nulo.

El campo tendrá componentes horizontal y vertical. La componente horizontal se anula por pura simetría aunque nada impide que la calculemos.

La definición de campo según la Wipikedia es

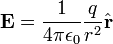
Dependiendo del nivel de estudios tal vez hayas dado una fórmula con menos carácter vectorial y con r en el denominador en lugar de r^2, pero esta está bien, el vector r compensa el r^2 del denominador.

Habrá que sumar los campos de las tres cargas e igualar al vector nulo.

Usaremos el subíndice 1 para la carga Q izquierda, el 2 para la carga Q derecha y el 3 para la de arriba.

Antes de nada yo no escribiré ni una sola vez más salvo esta el 1/(4·pi·epsilon_0)

Como tendremos la suma de tres vectores igualada a 0 y ese número es factor común de los tres vectores se simplifica y no hace falta para lo que vamos a calcular.

Tomaré como punto (0,0) la mitad de la base del triángulo

$$\begin{align}&\vec r_1=\left(0,-\frac a2\right)-\left(-\frac a2,0\right)=\left(\frac a2,-\frac a2\right)=\frac a2(1,-1)\\&\\&||\vec r_1||^2=\left(\frac a2\right)^2+\left(\frac a2\right)^2=\frac{a^2}{4}+\frac{a^2}{4}=\frac{a^2}{2}\\&\\&\\&\\&\vec r_2=\left(0,-\frac a2\right)-\left(\frac a2,0\right)=\left(-\frac a2,-\frac a2\right)=\frac a2(-1,-1)\\&\\&||\vec r_1||^2=\frac{a^2}{2}\\&\\&\\&\\&\vec r_3=\left(0,-\frac a2\right)-\left(0,a·sen 60º\right)=\left(\frac a2+\frac{\sqrt 3\;a}{2}  \right)(0,-1)=\\&\qquad \frac{(1+\sqrt 3)a}{2}(0,-1)\\&\\&||r_3||^2=\left(\frac{(1+\sqrt 3)a}{2}\right)^2\\&\\&\text{El campo generado por los tres igualado al vect r nulo es}\\&\\&\\&\frac{Q}{\frac {a^2}2}·\frac a2(1,-1)+\frac{Q}{\frac {a^2}2}·\frac a2(-1,-1)+\frac q{\left(\frac{(1+\sqrt 3)a}{2}\right)^2}\frac{(1+\sqrt 3)a}{2}(0,-1)=(0,0)\\&\\&\frac Qa(1,-1)+\frac{Q}{a}(-1,-1)+\frac{q}{\frac{(1+\sqrt 3)a}{2}}(0,-1)=(0,0)\\&\\&\text {descomponiendo}\\&\\&\frac Qa-\frac Qa =0 \implies 0=0\\&\text{lo que decia de que la componente horizontal era nula por simetria}\\&\\&-\frac Qa-\frac Qa-\frac{q}{\frac{(1+\sqrt 3)a}{2}}=0\\&\\&-2Q-\frac{q}{\frac{1+\sqrt 3}{2}}=0\\&\\&-2Q-\frac{2q}{1+\sqrt 3}=0\\&\\&Q+\frac{q}{1+\sqrt 3}=0\\&\\&Q = - \frac{q}{1+\sqrt 3}\\&\\&\frac Qq= -\frac{1}{1+\sqrt 3}=-\frac{1-\sqrt 3}{1-3}=-\frac{\sqrt 3 -1}{2}\approx -0.3660254038\\&\\&\end{align}$$

El signo - indica que Q y q son de signo contrario.